1/cos^2x Bằng Gì? Giải Đáp Chi Tiết và Ứng Dụng

1/cos²x bằng gì? Đây là một câu hỏi thường gặp trong lượng giác, và việc hiểu rõ câu trả lời cùng các ứng dụng của nó sẽ giúp bạn giải quyết nhiều bài toán phức tạp hơn. Bài viết này sẽ giải đáp chi tiết câu hỏi này, từ những kiến thức cơ bản nhất đến các ứng dụng thực tế, giúp bạn nắm vững công thức 1/cos²x và tự tin chinh phục các bài toán lượng giác.

Tìm Hiểu Về 1/cos²x

Vậy 1/cos²x bằng gì? Câu trả lời ngắn gọn là: 1/cos²x = sec²x. Secx (secant x) là nghịch đảo của cosx (cosin x). Nói cách khác, secx = 1/cosx. Do đó, 1/cos²x = (1/cosx)² = sec²x. Công thức này là một trong những hằng đẳng thức lượng giác cơ bản và được sử dụng rộng rãi trong việc giải các bài toán tích phân, đạo hàm, và các bài toán liên quan đến hình học.

Công thức 1/cos²x = sec²x

Chứng Minh Công Thức 1/cos²x = sec²x

Việc chứng minh công thức này khá đơn giản. Như đã đề cập, secx là nghịch đảo của cosx. Vậy, nếu bình phương cả hai vế của phương trình secx = 1/cosx, ta sẽ có sec²x = (1/cosx)² = 1/cos²x. Điều này chứng minh rằng 1/cos²x đúng bằng sec²x.

Ứng Dụng của 1/cos²x trong Đạo Hàm

Công thức 1/cos²x = sec²x có vai trò quan trọng trong việc tính đạo hàm. Đạo hàm của tanx (tang x) chính là sec²x, hay 1/cos²x. Điều này có nghĩa là khi bạn cần tính tích phân của sec²x, bạn sẽ có kết quả là tanx + C (C là hằng số).

Ứng Dụng của 1/cos²x trong Tích Phân

Như đã đề cập ở trên, vì đạo hàm của tanx là sec²x (1/cos²x), nên tích phân của sec²x sẽ là tanx + C. Đây là một ứng dụng quan trọng của công thức này trong giải tích. Việc nắm vững mối liên hệ giữa tanx, secx và 1/cos²x sẽ giúp bạn giải quyết các bài toán tích phân một cách nhanh chóng và hiệu quả.

Mối Liên Hệ Giữa 1/cos²x và Các Hằng Đẳng Thức Lượng Giác Khác

1/cos²x = sec²x cũng có mối liên hệ mật thiết với hằng đẳng thức lượng giác cơ bản: sin²x + cos²x = 1. Từ hằng đẳng thức này, chúng ta có thể suy ra nhiều công thức khác, bao gồm cả công thức liên quan đến 1/cos²x. Ví dụ, chia cả hai vế của sin²x + cos²x = 1 cho cos²x, ta được tan²x + 1 = 1/cos²x = sec²x.

Hằng đẳng thức lượng giác cơ bản

Ví Dụ Minh Họa về Ứng Dụng của 1/cos²x

Để hiểu rõ hơn về ứng dụng của công thức 1/cos²x, hãy xem xét một ví dụ cụ thể: Tính tích phân của ∫ sec²x dx. Như đã biết, tích phân của sec²x chính là tanx + C. Vậy, kết quả của tích phân này là tanx + C.

1/cos²x trong Hình Học

Trong hình học, 1/cos²x có thể được sử dụng để tính toán độ dài các cạnh và góc trong tam giác vuông. Ví dụ, trong một tam giác vuông, nếu biết góc x và cạnh kề, ta có thể tính cạnh huyền bằng cách sử dụng công thức cạnh huyền = cạnh kề secx = cạnh kề √(1/cos²x).

Ứng dụng 1/cos²x trong hình học

Bí Quyết Ghi Nhớ Công Thức 1/cos²x = sec²x

Một cách dễ nhớ công thức này là liên tưởng đến mối quan hệ nghịch đảo giữa cosx và secx. Hãy nhớ rằng secx là nghịch đảo của cosx, và khi bình phương cả hai vế, ta sẽ được 1/cos²x = sec²x. Bạn cũng có thể sử dụng các flashcards hoặc các phương pháp ghi nhớ khác để ghi nhớ công thức này một cách hiệu quả.

Giải Đáp Một Số Thắc Mắc Thường Gặp Về 1/cos²x

• 1/cos²x có giá trị âm không? Vì cos²x luôn dương (hoặc bằng 0), nên 1/cos²x cũng luôn dương (hoặc không xác định khi cosx = 0).
• Khi nào 1/cos²x không xác định? 1/cos²x không xác định khi cosx = 0, tức là khi x = π/2 + kπ (k là số nguyên).

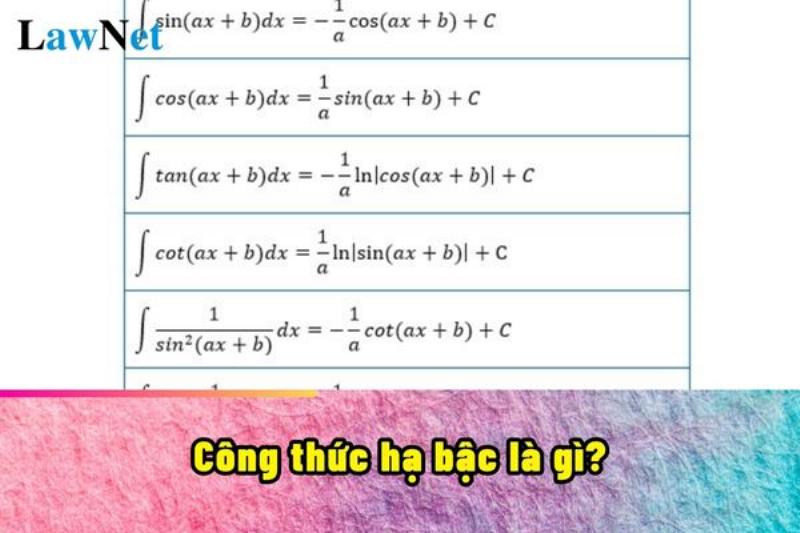Giải đáp thắc mắc về 1/cos²x

Kết Luận

Tóm lại, 1/cos²x bằng sec²x. Đây là một công thức lượng giác cơ bản và quan trọng, có ứng dụng rộng rãi trong giải tích, hình học và nhiều lĩnh vực khác. Hiểu rõ công thức này và các ứng dụng của nó sẽ giúp bạn giải quyết các bài toán lượng giác một cách hiệu quả hơn. Hãy thử áp dụng những kiến thức đã học vào bài tập và chia sẻ kinh nghiệm của bạn với chúng tôi!