Giải Ngay Bài Tập Biến Ngẫu Nhiên Liên Tục Có Lời Giải Chi Tiết

Chào bạn, có phải bạn đang “đau đầu” với môn Xác suất Thống kê, đặc biệt là phần biến ngẫu nhiên liên tục? Bạn tìm kiếm các ví dụ thực tế, những bài tập để luyện tay và quan trọng nhất là lời giải chi tiết để đối chiếu? Nếu câu trả lời là có, thì bạn đã đến đúng nơi rồi đấy. Trên Baocaothuctap.net, chúng tôi hiểu rõ những thách thức mà sinh viên thường gặp phải. Biến ngẫu nhiên liên tục là một khái niệm nền tảng nhưng không ít bạn cảm thấy khó “tiêu hóa” nó. Chính vì vậy, hôm nay chúng ta sẽ cùng nhau “mổ xẻ” và chinh phục nó qua tuyển tập Bài Tập Biến Ngẫu Nhiên Liên Tục Có Lời Giải cực kỳ đầy đủ và dễ hiểu. Mục tiêu của bài viết này không chỉ là cung cấp cho bạn các bài tập và đáp án, mà còn giúp bạn hiểu rõ gốc rễ vấn đề, từ đó tự tin giải quyết mọi bài toán liên quan đến biến ngẫu nhiên liên tục.

Bạn thấy đấy, việc nắm vững biến ngẫu nhiên liên tục không chỉ giúp bạn vượt qua các kỳ thi mà còn là nền tảng quan trọng cho nhiều lĩnh vực khác như kinh tế lượng, khoa học dữ liệu, kỹ thuật… “Trăm hay không bằng tay quen” – cách tốt nhất để thành thạo là thực hành. Và thực hành đúng cách là có người “cầm tay chỉ việc” qua những lời giải chi tiết. Đừng lo lắng nếu bạn cảm thấy bỡ ngỡ ban đầu, hành trình vạn dặm nào cũng bắt đầu từ bước chân đầu tiên. Hãy cùng tôi khám phá nhé!

Biến Ngẫu Nhiên Liên Tục Là Gì Mà Cần Nhiều Bài Tập Đến Thế?

Biến ngẫu nhiên liên tục (Continuous Random Variable) là một khái niệm cốt lõi trong Xác suất Thống kê. Nói một cách dễ hiểu nhất, nó là một biến mà giá trị của nó có thể là bất kỳ số thực nào trong một khoảng hoặc toàn bộ tập số thực. Khác với biến ngẫu nhiên rời rạc chỉ nhận các giá trị đếm được (như số mặt sấp khi tung đồng xu 5 lần: 0, 1, 2, 3, 4, 5), biến ngẫu nhiên liên tục có thể nhận vô số giá trị trong một khoảng cho trước.

Tưởng tượng cân nặng của một người, chiều cao của cây, thời gian chờ xe buýt, hay nhiệt độ không khí. Các đại lượng này không chỉ nhận một vài giá trị cố định mà có thể là 55.3 kg, 175.6 cm, 7.5 phút, 28.45 độ C… Giữa hai giá trị bất kỳ của biến ngẫu nhiên liên tục (ví dụ 55 kg và 56 kg), luôn tồn tại vô số giá trị khác (55.1 kg, 55.01 kg, 55.001 kg…). Chính vì đặc điểm này mà cách chúng ta tính xác suất cho biến ngẫu nhiên liên tục cũng khác biệt hoàn toàn so với biến ngẫu nhiên rời rạc, và đó là lý do bạn cần luyện tập nhiều bài tập biến ngẫu nhiên liên tục có lời giải.

Hàm Mật Độ Xác Suất (PDF) và Hàm Phân Phối Xác Suất (CDF) – Hai “Người Bạn” Quan Trọng

Với biến ngẫu nhiên liên tục, xác suất để biến nhận đúng một giá trị cụ thể (ví dụ: P(X = 55.3)) luôn bằng 0. Nghe có vẻ lạ lùng phải không? Hãy hình dung bạn đang cố tìm xác suất để một người nặng đúng 55.300000… kg với độ chính xác tuyệt đối. Điều này thực tế là không thể hoặc xác suất vô cùng nhỏ, tiệm cận 0. Do đó, chúng ta không làm việc với xác suất tại từng điểm như biến rời rạc, mà làm việc với xác suất trong một khoảng.

Đây là lúc Hàm Mật Độ Xác Suất (Probability Density Function – PDF), ký hiệu là f(x), và Hàm Phân Phối Xác Suất (Cumulative Distribution Function – CDF), ký hiệu là F(x), phát huy vai trò của mình.

• Hàm Mật Độ Xác Suất (f(x)): Hàm này mô tả “độ đậm đặc” xác suất tại mỗi điểm trên trục số. Giá trị của f(x) không phải là xác suất P(X=x), nhưng diện tích dưới đồ thị của f(x) trên một khoảng [a, b] chính là xác suất P(a ≤ X ≤ b).
  • Điều kiện của hàm mật độ f(x):
    • f(x) ≥ 0 với mọi x.
    • Diện tích toàn bộ dưới đồ thị f(x) phải bằng 1 (∫f(x)dx từ -∞ đến +∞ = 1).
• Hàm Phân Phối Xác Suất (F(x)): Hàm này cho biết xác suất để biến ngẫu nhiên X nhận giá trị nhỏ hơn hoặc bằng một giá trị x cụ thể, tức là F(x) = P(X ≤ x).
  • Mối liên hệ giữa F(x) và f(x): F(x) là nguyên hàm của f(x), và f(x) là đạo hàm của F(x) (f(x) = F'(x)).
  • Tính xác suất trong khoảng bằng CDF: P(a ≤ X ≤ b) = F(b) – F(a).

Nắm vững hai khái niệm này là chìa khóa để giải quyết mọi bài tập biến ngẫu nhiên liên tục có lời giải. Chúng ta sẽ thấy rõ điều này qua các ví dụ cụ thể sắp tới.

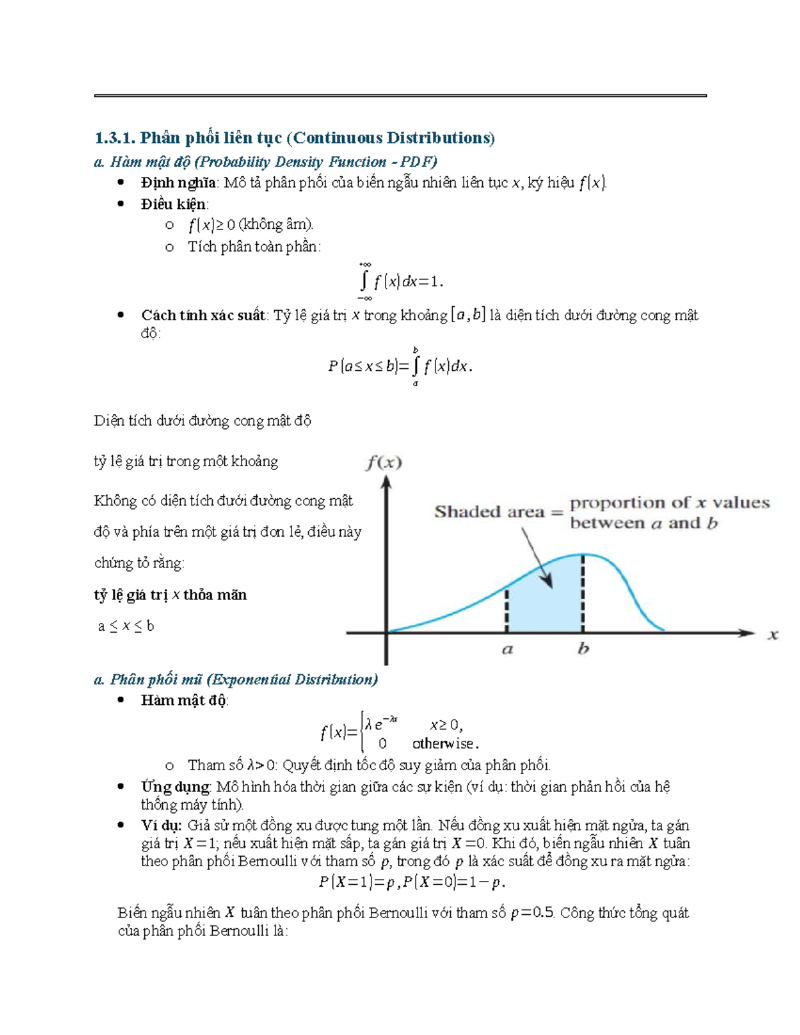Đồ thị minh họa hàm mật độ xác suất (PDF) và hàm phân phối xác suất (CDF) của biến ngẫu nhiên liên tục

Kỳ Vọng và Phương Sai – Những Chỉ Số Quan Trọng

Ngoài việc tính xác suất, chúng ta còn quan tâm đến các đặc trưng của biến ngẫu nhiên liên tục như giá trị trung bình (kỳ vọng) và độ phân tán (phương sai, độ lệch chuẩn).

• Kỳ Vọng (Expected Value), E(X) hoặc μ: Là giá trị trung bình “lý thuyết” của biến ngẫu nhiên. Nó cho biết giá trị “trung tâm” mà biến ngẫu nhiên có xu hướng xoay quanh.
  • Công thức tính: E(X) = ∫x * f(x) dx từ -∞ đến +∞.
• Phương Sai (Variance), Var(X) hoặc σ²: Đo lường mức độ phân tán của các giá trị biến ngẫu nhiên xung quanh kỳ vọng. Phương sai càng lớn, dữ liệu càng phân tán rộng.
  • Công thức tính: Var(X) = E(X²) – [E(X)]².
  • Trong đó, E(X²) = ∫x² * f(x) dx từ -∞ đến +∞.
• Độ Lệch Chuẩn (Standard Deviation), σ: Là căn bậc hai của phương sai. Nó có cùng đơn vị với biến ngẫu nhiên X và thường dễ diễn giải hơn phương sai.

Hiểu và tính toán được Kỳ vọng và Phương sai giúp chúng ta có cái nhìn sâu sắc hơn về tính chất của biến ngẫu nhiên đang xét. Các bài tập biến ngẫu nhiên liên tục có lời giải về phần này sẽ củng cố kiến thức của bạn.

Tại Sao Việc Giải Bài Tập Biến Ngẫu Nhiên Liên Tục Có Lời Giải Lại Quan Trọng?

Bạn có thể tự hỏi, tại sao tôi không chỉ đọc lý thuyết và công thức là đủ? Câu trả lời rất đơn giản: Lý thuyết là nền tảng, nhưng bài tập là cách bạn biến lý thuyết thành kiến thức của mình. Giống như học bơi, bạn có thể đọc sách dạy bơi cả ngày, nhưng bạn chỉ thực sự biết bơi khi nhảy xuống nước và bắt đầu quạt tay.

• Kiểm tra sự hiểu biết: Khi giải bài tập, bạn buộc phải vận dụng công thức và khái niệm. Nếu giải sai, lời giải chi tiết sẽ chỉ cho bạn biết bạn đã hiểu sai ở đâu, từ đó lấp đầy lỗ hổng kiến thức.
• Làm quen với các dạng bài: Biến ngẫu nhiên liên tục có nhiều dạng bài khác nhau: tìm hằng số, tính xác suất trong khoảng, tính kỳ vọng/phương sai, bài toán ứng dụng… Luyện tập giúp bạn nhận diện và biết cách xử lý từng dạng.
• Tăng tốc độ và độ chính xác: Càng làm nhiều, bạn càng quen tay với các phép tính tích phân, đạo hàm, và các bước lập luận. Điều này giúp bạn giải quyết bài tập nhanh hơn và chính xác hơn trong phòng thi.
• Xây dựng sự tự tin: Mỗi bài tập bạn giải được, đặc biệt là những bài khó, đều tăng thêm sự tự tin cho bạn khi đối mặt với chủ đề này.

Đó là lý do vì sao chúng tôi đặc biệt chú trọng vào việc cung cấp bài tập biến ngẫu nhiên liên tục có lời giải một cách đầy đủ và chi tiết nhất.

Các Dạng Bài Tập Biến Ngẫu Nhiên Liên Tục Thường Gặp (Kèm Lời Giải)

Giờ là lúc chúng ta “xắn tay áo” và bắt đầu với phần chính: các dạng bài tập biến ngẫu nhiên liên tục có lời giải thường xuất hiện trong các đề thi hoặc bài kiểm tra. Chúng ta sẽ đi từ cơ bản đến nâng cao, đảm bảo bạn nắm vững từng bước.

Dạng 1: Tìm Hằng Số Từ Hàm Mật Độ Xác Suất (f(x))

Đây là dạng bài tập nền tảng nhất. Bạn được cho một hàm f(x) chứa một hằng số chưa biết (thường là c, k, a, b…) và nhiệm vụ của bạn là tìm giá trị của hằng số đó dựa vào điều kiện của hàm mật độ xác suất.

• Câu hỏi thường gặp: Cho hàm f(x) = { k * g(x) nếu x thuộc [a, b]; 0 nếu ngược lại }. Tìm k để f(x) là hàm mật độ xác suất.
• Cách giải nhanh: Sử dụng điều kiện ∫f(x)dx từ -∞ đến +∞ = 1. Do f(x) = 0 ngoài khoảng [a, b], tích phân chỉ cần tính trong khoảng này: ∫[a, b] k * g(x) dx = 1. Từ đó suy ra k.

Minh họa bài toán tìm hằng số k trong hàm mật độ xác suất của biến ngẫu nhiên liên tục and 0 elsewhere. Show the integral formula ∫f(x)dx = 1 and the step of setting up the integral over the interval [a, b] to solve for k.]

Bài Tập 1: Tìm Hằng Số k

Đề bài: Cho hàm số f(x) như sau:
f(x) = { kx² nếu 0 ≤ x ≤ 3
f(x) = { 0 nếu ngược lại

Tìm giá trị của hằng số k để f(x) là hàm mật độ xác suất của một biến ngẫu nhiên liên tục X.

Lời giải chi tiết:

Để f(x) là hàm mật độ xác suất, nó cần thỏa mãn hai điều kiện:

1. f(x) ≥ 0 với mọi x.
2. ∫f(x)dx từ -∞ đến +∞ = 1.

Điều kiện 1: kx² ≥ 0 với 0 ≤ x ≤ 3. Do x² ≥ 0 trong khoảng này, để f(x) ≥ 0 thì k phải không âm, tức là k ≥ 0.

Điều kiện 2: Tích phân của f(x) trên toàn bộ trục số phải bằng 1. Do f(x) chỉ khác 0 trong khoảng [0, 3], ta chỉ cần tính tích phân trên khoảng này:
∫[-∞, +∞] f(x) dx = ∫[0, 3] kx² dx = 1

Tính tích phân:
∫[0, 3] kx² dx = k ∫[0, 3] x² dx
= k [x³/3] từ 0 đến 3
= k ((3³/3) – (0³/3))
= k (27/3 – 0)
= k * 9

Vậy ta có phương trình: 9k = 1
Suy ra k = 1/9.

Giá trị k = 1/9 thỏa mãn điều kiện k ≥ 0.

Kết luận: Giá trị của hằng số k để f(x) là hàm mật độ xác suất là k = 1/9.
Hàm mật độ xác suất đầy đủ là:
f(x) = { x²/9 nếu 0 ≤ x ≤ 3
f(x) = { 0 nếu ngược lại

Đây là một ví dụ cơ bản trong các bài tập biến ngẫu nhiên liên tục có lời giải, giúp bạn làm quen với điều kiện tiên quyết của hàm mật độ.

Dạng 2: Tính Xác Suất Từ Hàm Mật Độ (f(x)) hoặc Hàm Phân Phối (F(x))

Đây là dạng bài tập thường gặp nhất, yêu cầu bạn tính xác suất để biến ngẫu nhiên liên tục X nhận giá trị trong một khoảng [a, b].

• Câu hỏi thường gặp: Cho hàm mật độ f(x) hoặc hàm phân phối F(x). Tính P(c ≤ X ≤ d), P(X > c), P(X < d), P(X = c).
• Cách giải nhanh:
  • P(c ≤ X ≤ d) = ∫[c, d] f(x) dx. Nếu có F(x), P(c ≤ X ≤ d) = F(d) – F(c).
  • P(X > c) = ∫[c, +∞] f(x) dx = 1 – F(c).
  • P(X < d) = ∫[-∞, d] f(x) dx = F(d).
  • P(X = c) = 0 cho bất kỳ biến ngẫu nhiên liên tục nào.

Bài Tập 2: Tính Xác Suất Từ Hàm Mật Độ

Đề bài: Cho biến ngẫu nhiên liên tục X có hàm mật độ xác suất f(x):
f(x) = { 2x nếu 0 ≤ x ≤ 1
f(x) = { 0 nếu ngược lại

a) Tính P(0.2 ≤ X ≤ 0.8)
b) Tính P(X > 0.5)

Lời giải chi tiết:

a) Tính P(0.2 ≤ X ≤ 0.8):
Xác suất để X nằm trong khoảng [0.2, 0.8] được tính bằng tích phân của hàm mật độ f(x) trên khoảng này. Cả 0.2 và 0.8 đều nằm trong khoảng [0, 1] nơi f(x) = 2x.
P(0.2 ≤ X ≤ 0.8) = ∫[0.2, 0.8] f(x) dx
= ∫[0.2, 0.8] 2x dx
= [x²] từ 0.2 đến 0.8
= (0.8)² – (0.2)²
= 0.64 – 0.04
= 0.60

b) Tính P(X > 0.5):
Xác suất để X lớn hơn 0.5 được tính bằng tích phân của f(x) từ 0.5 đến +∞. Hàm f(x) chỉ khác 0 trong khoảng [0, 1]. Do đó, tích phân chỉ cần tính từ 0.5 đến 1.
P(X > 0.5) = ∫[0.5, +∞] f(x) dx
= ∫[0.5, 1] 2x dx + ∫[1, +∞] 0 dx
= ∫[0.5, 1] 2x dx
= [x²] từ 0.5 đến 1
= (1)² – (0.5)²
= 1 – 0.25
= 0.75

Kết luận:
a) P(0.2 ≤ X ≤ 0.8) = 0.60
b) P(X > 0.5) = 0.75

Các bài tập biến ngẫu nhiên liên tục có lời giải dạng này đòi hỏi kỹ năng tính tích phân cơ bản.

Bài Tập 3: Tính Xác Suất Từ Hàm Phân Phối

Đề bài: Cho biến ngẫu nhiên liên tục X có hàm phân phối xác suất F(x):
F(x) = { 0 nếu x < 0
F(x) = { x²/4 nếu 0 ≤ x ≤ 2
F(x) = { 1 nếu x > 2

a) Tính P(X ≤ 1)
b) Tính P(X > 1.5)
c) Tính P(0.5 ≤ X ≤ 1.5)

Lời giải chi tiết:

Hàm phân phối F(x) cho trực tiếp xác suất P(X ≤ x).
a) Tính P(X ≤ 1):
Theo định nghĩa của F(x), P(X ≤ 1) chính là F(1). Giá trị x = 1 nằm trong khoảng [0, 2], nên ta sử dụng công thức F(x) = x²/4.
P(X ≤ 1) = F(1) = (1)²/4 = 1/4 = 0.25.

b) Tính P(X > 1.5):
Xác suất P(X > 1.5) có thể tính bằng 1 – P(X ≤ 1.5). P(X ≤ 1.5) chính là F(1.5). Giá trị x = 1.5 nằm trong khoảng [0, 2], nên ta sử dụng công thức F(x) = x²/4.
P(X > 1.5) = 1 – F(1.5) = 1 – (1.5)²/4 = 1 – (2.25)/4 = 1 – 0.5625 = 0.4375.

c) Tính P(0.5 ≤ X ≤ 1.5):
Xác suất P(0.5 ≤ X ≤ 1.5) được tính bằng hiệu của hai giá trị hàm phân phối: F(1.5) – F(0.5).
Cả 0.5 và 1.5 đều nằm trong khoảng [0, 2], nên ta sử dụng công thức F(x) = x²/4 cho cả hai.
P(0.5 ≤ X ≤ 1.5) = F(1.5) – F(0.5)
= (1.5)²/4 – (0.5)²/4
= (2.25)/4 – (0.25)/4
= (2.25 – 0.25) / 4
= 2 / 4
= 0.5.

Kết luận:
a) P(X ≤ 1) = 0.25
b) P(X > 1.5) = 0.4375
c) P(0.5 ≤ X ≤ 1.5) = 0.5

Giải các bài tập biến ngẫu nhiên liên tục có lời giải dùng hàm phân phối thường đơn giản hơn so với dùng hàm mật độ nếu bạn đã có sẵn F(x).

Dạng 3: Tìm Kỳ Vọng, Phương Sai và Độ Lệch Chuẩn

Dạng bài tập này yêu cầu bạn tính các đặc trưng của biến ngẫu nhiên dựa vào hàm mật độ f(x).

• Câu hỏi thường gặp: Cho hàm mật độ f(x). Tính E(X), Var(X), σ(X).
• Cách giải nhanh: Áp dụng trực tiếp công thức tích phân cho E(X) và E(X²), sau đó dùng công thức Var(X) = E(X²) – [E(X)]² và σ(X) = √Var(X).

Bài Tập 4: Tính Kỳ Vọng và Phương Sai

Đề bài: Cho biến ngẫu nhiên liên tục X có hàm mật độ xác suất f(x):
f(x) = { (1/2)x nếu 0 ≤ x ≤ 2
f(x) = { 0 nếu ngược lại

Tính Kỳ vọng E(X) và Phương sai Var(X) của X.

Lời giải chi tiết:

Bước 1: Tính Kỳ vọng E(X).
Áp dụng công thức E(X) = ∫[-∞, +∞] x f(x) dx. Do f(x) chỉ khác 0 trong khoảng [0, 2], tích phân chỉ cần tính trong khoảng này.
E(X) = ∫[0, 2] x (1/2)x dx
= ∫[0, 2] (1/2)x² dx
= (1/2) ∫[0, 2] x² dx
= (1/2) [x³/3] từ 0 đến 2
= (1/2) ((2³/3) – (0³/3))
= (1/2) (8/3 – 0)
= (1/2) * (8/3)
= 4/3.

Bước 2: Tính E(X²).
Áp dụng công thức E(X²) = ∫[-∞, +∞] x² f(x) dx. Tương tự, tích phân tính trên khoảng [0, 2].
E(X²) = ∫[0, 2] x² (1/2)x dx
= ∫[0, 2] (1/2)x³ dx
= (1/2) ∫[0, 2] x³ dx
= (1/2) [x⁴/4] từ 0 đến 2
= (1/2) ((2⁴/4) – (0⁴/4))
= (1/2) (16/4 – 0)
= (1/2) * 4
= 2.

Bước 3: Tính Phương sai Var(X).
Áp dụng công thức Var(X) = E(X²) – [E(X)]².
Var(X) = 2 – (4/3)²
= 2 – 16/9
= 18/9 – 16/9
= 2/9.

Kết luận:
Kỳ vọng E(X) = 4/3
Phương sai Var(X) = 2/9

Để giải tốt các bài tập biến ngẫu nhiên liên tục có lời giải về Kỳ vọng và Phương sai, bạn cần thành thạo việc tính tích phân của các hàm lũy thừa.

Dạng 4: Xác định Hàm Phân Phối (F(x)) từ Hàm Mật Độ (f(x)) và Ngược Lại

Đôi khi đề bài cho hàm mật độ và yêu cầu tìm hàm phân phối, hoặc ngược lại.

• Câu hỏi thường gặp: Cho f(x), tìm F(x). Hoặc cho F(x), tìm f(x).
• Cách giải nhanh:
  • f(x) -> F(x): F(x) = ∫[-∞, x] f(t) dt. Lưu ý hàm F(x) luôn có dạng phân nhánh và F(x) = 0 với x < giá trị nhỏ nhất của miền xác định của X, và F(x) = 1 với x > giá trị lớn nhất của miền xác định của X.
  • F(x) -> f(x): f(x) = F'(x). Lấy đạo hàm của F(x) theo x.

Mối quan hệ giữa hàm mật độ xác suất và hàm phân phối xác suất

Bài Tập 5: Tìm Hàm Phân Phối từ Hàm Mật Độ

Đề bài: Tìm hàm phân phối F(x) của biến ngẫu nhiên liên tục X có hàm mật độ f(x) đã cho trong Bài tập 4:
f(x) = { (1/2)x nếu 0 ≤ x ≤ 2
f(x) = { 0 nếu ngược lại

Lời giải chi tiết:

Theo định nghĩa, F(x) = P(X ≤ x) = ∫[-∞, x] f(t) dt.
Ta xét các khoảng giá trị của x:

Trường hợp 1: x < 0
Trong khoảng này, f(t) = 0 với mọi t < x.
F(x) = ∫[-∞, x] 0 dt = 0.

Trường hợp 2: 0 ≤ x ≤ 2
Trong khoảng này, tích phân từ -∞ đến x được chia thành hai phần: từ -∞ đến 0 (nơi f(t)=0) và từ 0 đến x (nơi f(t) = (1/2)t).
F(x) = ∫[-∞, x] f(t) dt = ∫[-∞, 0] 0 dt + ∫[0, x] (1/2)t dt
F(x) = 0 + (1/2) ∫[0, x] t dt
F(x) = (1/2) [t²/2] từ 0 đến x
F(x) = (1/2) * (x²/2 – 0²/2)
F(x) = x²/4.

Trường hợp 3: x > 2
Trong khoảng này, toàn bộ miền xác định của X (từ 0 đến 2) đã nằm bên trái x. Tích phân từ -∞ đến x bao gồm tích phân trên toàn bộ miền xác định [0, 2] và phần còn lại từ 2 đến x (nơi f(t)=0).
F(x) = ∫[-∞, x] f(t) dt = ∫[-∞, 0] 0 dt + ∫[0, 2] (1/2)t dt + ∫[2, x] 0 dt
F(x) = 0 + ∫[0, 2] (1/2)t dt + 0
Tích phân ∫[0, 2] (1/2)t dt chính là tích phân của hàm mật độ trên toàn bộ miền xác định, và giá trị của nó phải bằng 1 (điều kiện của hàm mật độ).
F(x) = 1.

Kết hợp các trường hợp, ta có hàm phân phối F(x):
F(x) = { 0 nếu x < 0
F(x) = { x²/4 nếu 0 ≤ x ≤ 2
F(x) = { 1 nếu x > 2

Kết luận: Hàm phân phối xác suất là F(x) như trên.
Bạn có thể kiểm tra lại bằng cách lấy đạo hàm F'(x).
Nếu 0 < x < 2, F'(x) = d(x²/4)/dx = 2x/4 = x/2 = (1/2)x, chính là f(x).
Tại các điểm gián đoạn (0 và 2), hàm mật độ không xác định giá trị, nên việc đạo hàm tại đó không cần thiết.
F(x) tăng từ 0 đến 1, liên tục (trừ tại các điểm nối nếu hàm mật độ gián đoạn).

Việc thành thạo chuyển đổi giữa f(x) và F(x) là rất quan trọng khi làm các bài tập biến ngẫu nhiên liên tục có lời giải phức tạp hơn.

Dạng 5: Bài Toán Ứng Dụng Thực Tế

Biến ngẫu nhiên liên tục xuất hiện rất nhiều trong đời sống và các ngành khoa học. Các bài tập dạng này thường mô tả một tình huống thực tế và yêu cầu bạn xây dựng hoặc sử dụng hàm mật độ/phân phối để tính toán.

• Ví dụ: Thời gian phục vụ khách hàng, tuổi thọ thiết bị, sai số đo lường, nồng độ hóa chất… thường được mô hình hóa bằng biến ngẫu nhiên liên tục với các phân phối cụ thể như phân phối đều, phân phối mũ, phân phối chuẩn…

Bài Tập 6: Ứng dụng Phân phối Đều (Uniform Distribution)

Đề bài: Thời gian chờ xe buýt tại một trạm được mô hình hóa bởi một biến ngẫu nhiên liên tục X (đơn vị: phút) có phân phối đều trên khoảng [0, 15]. Tức là, hành khách có thể phải chờ bất kỳ lúc nào từ 0 đến 15 phút với xác suất như nhau cho mỗi khoảng thời gian có độ dài bằng nhau trong [0, 15].
a) Viết hàm mật độ xác suất f(x) của X.
b) Tính xác suất hành khách phải chờ hơn 10 phút.
c) Tính thời gian chờ trung bình (kỳ vọng).

Lời giải chi tiết:

Biến ngẫu nhiên X có phân phối đều trên khoảng [a, b], với a = 0, b = 15.

a) Hàm mật độ xác suất của phân phối đều trên [a, b] có công thức:
f(x) = { 1/(b-a) nếu a ≤ x ≤ b
f(x) = { 0 nếu ngược lại

Thay a=0, b=15:
f(x) = { 1/(15-0) nếu 0 ≤ x ≤ 15
f(x) = { 0 nếu ngược lại

f(x) = { 1/15 nếu 0 ≤ x ≤ 15
f(x) = { 0 nếu ngược lại

b) Tính xác suất hành khách phải chờ hơn 10 phút. Tức là tính P(X > 10).
Đây là xác suất để X nhận giá trị trong khoảng (10, +∞). Dựa vào hàm mật độ, ta chỉ cần tích phân f(x) từ 10 đến 15 (vì ngoài khoảng [0, 15], f(x)=0).
P(X > 10) = ∫[10, +∞] f(x) dx
= ∫[10, 15] (1/15) dx + ∫[15, +∞] 0 dx
= (1/15) ∫[10, 15] dx
= (1/15) [x] từ 10 đến 15
= (1/15) (15 – 10)
= (1/15) 5
= 5/15
= 1/3.

c) Tính thời gian chờ trung bình (kỳ vọng E(X)).
Áp dụng công thức E(X) = ∫[-∞, +∞] x f(x) dx. Tích phân trên khoảng [0, 15].
E(X) = ∫[0, 15] x (1/15) dx
= (1/15) ∫[0, 15] x dx
= (1/15) [x²/2] từ 0 đến 15
= (1/15) (15²/2 – 0²/2)
= (1/15) (225/2)
= 225 / 30
= 15/2 = 7.5.

Kết luận:
a) Hàm mật độ xác suất: f(x) = 1/15 cho 0 ≤ x ≤ 15, và 0 ngược lại.
b) Xác suất chờ hơn 10 phút là 1/3.
c) Thời gian chờ trung bình là 7.5 phút.

Bài tập dạng ứng dụng giúp bạn thấy được sự hữu ích của biến ngẫu nhiên liên tục trong việc mô hình hóa các hiện tượng ngẫu nhiên trong cuộc sống. Việc giải các bài tập biến ngẫu nhiên liên tục có lời giải này giúp bạn kết nối lý thuyết với thực tế.

Dạng 6: Biến Đổi Biến Ngẫu Nhiên

Đôi khi bạn có một biến ngẫu nhiên liên tục X và định nghĩa một biến ngẫu nhiên mới Y = g(X), trong đó g là một hàm số. Bạn cần tìm hàm mật độ hoặc hàm phân phối của Y.

• Câu hỏi thường gặp: Cho f_X(x), tìm f_Y(y) khi Y = g(X).
• Cách giải nhanh: Sử dụng phương pháp hàm phân phối hoặc phương pháp biến đổi. Phương pháp hàm phân phối thường đơn giản hơn: Tìm F_Y(y) = P(Y ≤ y) = P(g(X) ≤ y). Biểu diễn sự kiện g(X) ≤ y dưới dạng một điều kiện trên X, ví dụ X ≤ h(y) nếu g là hàm tăng đơn điệu. Khi đó F_Y(y) = P(X ≤ h(y)) = F_X(h(y)). Cuối cùng, tìm f_Y(y) = F’_Y(y). Nếu g không đơn điệu, cần xét cẩn thận hơn.

Bài Tập 7: Biến Đổi Biến Ngẫu Nhiên

Đề bài: Cho biến ngẫu nhiên liên tục X có hàm mật độ xác suất đều trên khoảng (0, 1), tức là f_X(x) = { 1 nếu 0 < x < 1; 0 nếu ngược lại }.
Xét biến ngẫu nhiên Y = -2ln(X). Tìm hàm mật độ xác suất f_Y(y) của Y.

Lời giải chi tiết:

Bước 1: Tìm miền giá trị của Y.
Vì 0 < X < 1, ta có:
ln(X) < ln(1) = 0
-2ln(X) > -2 * 0 = 0
Vậy, miền giá trị của Y là (0, +∞).

Bước 2: Tìm hàm phân phối F_Y(y) của Y.
F_Y(y) = P(Y ≤ y) = P(-2ln(X) ≤ y)

Xét y trong miền giá trị của Y, tức y > 0:
-2ln(X) ≤ y
ln(X) ≥ -y/2
X ≥ e^(-y/2)

Vậy, F_Y(y) = P(X ≥ e^(-y/2)).
Vì X có phân phối đều trên (0, 1), hàm phân phối của X là F_X(x) = P(X ≤ x) = x cho 0 < x < 1.
P(X ≥ e^(-y/2)) = 1 – P(X < e^(-y/2)) = 1 – P(X ≤ e^(-y/2)) (vì X liên tục).
P(X ≤ e^(-y/2)) = F_X(e^(-y/2)).

Để F_X(e^(-y/2)) có nghĩa, e^(-y/2) phải nằm trong khoảng (0, 1).
Vì y > 0, -y/2 < 0, nên e^(-y/2) < e^0 = 1.
Và e^(-y/2) luôn > 0.
Vậy, e^(-y/2) luôn nằm trong khoảng (0, 1) khi y > 0.

Do đó, F_X(e^(-y/2)) = e^(-y/2) cho y > 0.

F_Y(y) = 1 – e^(-y/2) cho y > 0.
Nếu y ≤ 0, P(Y ≤ y) = P(-2ln(X) ≤ y). Vì Y > 0, xác suất này bằng 0.
Vậy, hàm phân phối của Y là:
F_Y(y) = { 0 nếu y ≤ 0
F_Y(y) = { 1 – e^(-y/2) nếu y > 0

Bước 3: Tìm hàm mật độ f_Y(y) của Y bằng cách lấy đạo hàm của F_Y(y).
f_Y(y) = F’_Y(y)

Nếu y ≤ 0, F_Y(y) = 0, nên f_Y(y) = 0.
Nếu y > 0, F_Y(y) = 1 – e^(-y/2).
f_Y(y) = d/dy (1 – e^(-y/2))
= 0 – e^(-y/2) d/dy (-y/2)
= – e^(-y/2) (-1/2)
= (1/2)e^(-y/2).

Kết hợp các trường hợp, ta có hàm mật độ xác suất của Y:
f_Y(y) = { (1/2)e^(-y/2) nếu y > 0
f_Y(y) = { 0 nếu y ≤ 0

Kết luận: Hàm mật độ xác suất của Y là f_Y(y) như trên. Đây chính là hàm mật độ của phân phối mũ với tham số λ = 1/2.

Dạng bài tập này yêu cầu sự kết hợp giữa kiến thức về biến ngẫu nhiên và kỹ năng về hàm ngược, đạo hàm, tích phân. Giải được các bài tập biến ngẫu nhiên liên tục có lời giải dạng này cho thấy bạn đã nắm vững kiến thức ở mức độ cao hơn.

Làm Thế Nào Để Học Tốt Biến Ngẫu Nhiên Liên Tục?

Học tốt Biến ngẫu nhiên liên tục không phải là một điều quá khó khăn nếu bạn có phương pháp đúng đắn. Dưới đây là một vài lời khuyên từ những người đi trước:

Nắm Vững Lý Thuyết Gốc Rễ

Đừng vội vàng lao vào giải bài tập nếu bạn chưa hiểu rõ các khái niệm cơ bản: Hàm mật độ nghĩa là gì? Tại sao xác suất tại một điểm lại bằng 0? Mối liên hệ giữa hàm mật độ và hàm phân phối là gì? Kỳ vọng và phương sai cho ta biết điều gì về biến ngẫu nhiên? Khi đã hiểu rõ “gốc rễ”, bạn sẽ không bị bối rối khi gặp các dạng bài lạ.

Luyện Tập Thường Xuyên và Có Hệ Thống

Đây là lời khuyên quan trọng nhất. Giống như bất kỳ kỹ năng nào, bạn cần luyện tập để thành thạo. Hãy bắt đầu từ những bài tập biến ngẫu nhiên liên tục có lời giải cơ bản nhất (tìm hằng số, tính xác suất đơn giản), sau đó tăng dần độ khó (tính kỳ vọng/phương sai của hàm phức tạp hơn, bài toán biến đổi biến ngẫu nhiên, bài toán ứng dụng thực tế). Việc luyện tập có hệ thống giúp bạn củng cố kiến thức từng bước và không bỏ sót dạng bài nào.

Đừng Ngại Ngừng Với Tích Phân và Đạo Hàm

Các phép toán tích phân và đạo hàm là công cụ không thể thiếu khi làm việc với biến ngẫu nhiên liên tục. Nếu bạn cảm thấy mình còn yếu ở phần này, hãy dành thời gian ôn tập lại kiến thức giải tích liên quan. Đôi khi, việc giải sai bài tập không phải do bạn không hiểu xác suất, mà là do tính tích phân/đạo hàm bị nhầm lẫn.

Hiểu Bản Chất Vấn Đề, Đừng Chỉ Học Thuộc Lòng

Mỗi bài tập đều có “cái hồn” riêng của nó. Hãy cố gắng hiểu xem bài toán đang mô tả hiện tượng gì, tại sao lại sử dụng mô hình biến ngẫu nhiên liên tục, và kết quả tính toán của bạn có ý nghĩa thực tế nào. Việc hiểu bản chất giúp bạn áp dụng linh hoạt kiến thức vào các tình huống mới, thay vì chỉ giải được những bài giống hệt ví dụ mẫu.

Lời Khuyên Từ Chuyên Gia

Chúng tôi đã có dịp trò chuyện với Tiến sĩ Nguyễn Thị Mai, một chuyên gia uy tín trong lĩnh vực Xác suất Thống kê tại Việt Nam. Bà chia sẻ:

“Nhiều sinh viên xem biến ngẫu nhiên liên tục là một ‘cơn ác mộng’ chỉ vì họ ngại việc tính toán với tích phân. Thực ra, các bài toán cơ bản chỉ đòi hỏi những kỹ năng giải tích không quá phức tạp. Điều quan trọng là bạn phải hiểu rõ ý nghĩa vật lý của các khái niệm: diện tích dưới đường cong là xác suất, kỳ vọng là ‘điểm cân bằng’ của phân phối. Hãy bắt đầu với những bài tập cơ bản có lời giải chi tiết, tự tay làm lại từng bước, và đừng bỏ qua bất kỳ chỗ nào bạn chưa thực sự hiểu. Dần dần, bạn sẽ thấy mọi thứ trở nên dễ dàng hơn rất nhiều.”

Lời khuyên của Tiến sĩ Mai nhấn mạnh tầm quan trọng của việc kết hợp giữa hiểu lý thuyết và thực hành có phương pháp với bài tập biến ngẫu nhiên liên tục có lời giải.

Tóm Lại

Biến ngẫu nhiên liên tục là một chủ đề quan trọng và thú vị trong Xác suất Thống kê. Để nắm vững nó, bạn cần hiểu rõ các khái niệm như hàm mật độ, hàm phân phối, kỳ vọng, phương sai, và luyện tập thường xuyên với nhiều dạng bài tập khác nhau.

Trong bài viết này, chúng tôi đã cùng nhau đi qua các dạng bài tập biến ngẫu nhiên liên tục có lời giải từ cơ bản đến nâng cao, bao gồm:

• Tìm hằng số từ hàm mật độ.
• Tính xác suất từ hàm mật độ và hàm phân phối.
• Tính kỳ vọng và phương sai.
• Xác định hàm phân phối từ hàm mật độ và ngược lại.
• Bài toán ứng dụng thực tế.
• Bài toán biến đổi biến ngẫu nhiên.

Mỗi bài tập đều đi kèm lời giải chi tiết, giúp bạn dễ dàng theo dõi và tự kiểm tra.

Hãy xem những bài tập này là điểm khởi đầu cho hành trình làm chủ biến ngẫu nhiên liên tục của bạn. Đừng chỉ đọc lời giải, hãy thử tự mình giải trước, sau đó mới đối chiếu. Tìm thêm các bài tập biến ngẫu nhiên liên tục có lời giải khác từ sách giáo khoa, tài liệu tham khảo, hoặc các nguồn đáng tin cậy trên mạng để đa dạng hóa việc luyện tập.

Chúng tôi hy vọng rằng với nguồn tài nguyên về bài tập biến ngẫu nhiên liên tục có lời giải này, bạn sẽ cảm thấy tự tin hơn rất nhiều khi đối mặt với chủ đề này. Chúc bạn học tốt và đạt được kết quả cao!