Bài tập đại số tuyến tính có lời giải: Chìa khóa làm chủ môn Toán

Bạn đang vật lộn với ma trận, định thức, không gian vector hay những ánh xạ tuyến tính “lằng nhằng” trong môn Đại số Tuyến tính? Cảm giác như đang lạc vào một mê cung toàn số và ký hiệu khó hiểu? Đừng lo, bạn không đơn độc đâu. Rất nhiều sinh viên xem Đại số Tuyến tính là một trong những môn “khó nhằn” nhất trong chương trình đại học. Lý thuyết thì trừu tượng, công thức thì chồng chất, và khi bắt tay vào làm bài tập thì… ôi thôi, cứ sai lên sai xuống.

Nhưng nếu tôi nói với bạn rằng có một “chìa khóa” giúp bạn mở cánh cửa hiểu biết và làm chủ môn học này một cách hiệu quả hơn rất nhiều thì sao? Chìa khóa đó chính là Bài Tập đại Số Tuyến Tính Có Lời Giải. Vâng, nghe có vẻ đơn giản, nhưng sức mạnh của việc luyện tập đúng cách với những bài tập đã có lời giải chi tiết là không thể xem thường. Chúng không chỉ giúp bạn kiểm tra lại kết quả, mà quan trọng hơn, giúp bạn “thông não” quy trình suy luận, áp dụng công thức và tránh những sai lầm phổ biến. Hãy cùng Baocaothuctap.net khám phá sâu hơn về bí quyết này nhé!

Tại sao bài tập đại số tuyến tính có lời giải lại quan trọng đến vậy?

Bài tập có lời giải đóng vai trò như một người thầy thầm lặng, chỉ dẫn bạn đi đúng hướng.

Nó giúp bạn củng cố lý thuyết vừa học bằng cách áp dụng trực tiếp vào bài toán cụ thể. Khi bạn tự giải rồi đối chiếu với lời giải, bạn sẽ thấy mình sai ở đâu, vướng mắc chỗ nào. Quá trình này hiệu quả hơn nhiều so với việc chỉ đọc lại lý thuyết suông. Tương tự như việc xây dựng một nền tảng vững chắc, dù là trong học tập hay cuộc sống, bạn cần có những viên gạch lý thuyết vững chắc và vữa thực hành kết dính. Việc tìm hiểu về các chủ đề học thuật như sách chủ nghĩa xã hội khoa học hay các môn lý luận khác cũng đòi hỏi sự kết hợp giữa nắm vững nguyên lý và khả năng phân tích thực tế.

Bài tập có lời giải giúp ích gì cho việc học của bạn?

Chúng cung cấp một con đường rõ ràng để bạn kiểm tra sự hiểu biết của mình và học hỏi từ những sai lầm.

Việc có lời giải giúp bạn tự học hiệu quả hơn, không bị bế tắc quá lâu khi gặp bài khó. Bạn có thể xem lời giải như một gợi ý, hoặc chỉ dùng nó để kiểm tra lại đáp án sau khi đã tự giải xong. Điều này tạo ra một vòng lặp học tập tích cực: làm bài -> kiểm tra -> hiểu sai lầm -> làm lại hoặc làm bài khác tương tự.

Những dạng bài tập đại số tuyến tính thường gặp là gì?

Đại số Tuyến tính bao trùm nhiều chủ đề, từ cơ bản đến nâng cao.

Các dạng bài tập phổ biến bao gồm: tính toán ma trận (cộng, trừ, nhân, tìm ma trận nghịch đảo), tính định thức, giải hệ phương trình tuyến tính (bằng phương pháp Gauss, Cramer, ma trận nghịch đảo), tìm hạng ma trận, làm việc với không gian vector (kiểm tra độc lập tuyến tính, tìm cơ sở, chiều, tọa độ), ánh xạ tuyến tính (tìm ma trận biểu diễn, kernel, image), và các bài toán về trị riêng, vector riêng, dạng toàn phương. Mỗi dạng có những kỹ thuật và công thức riêng cần nắm vững.

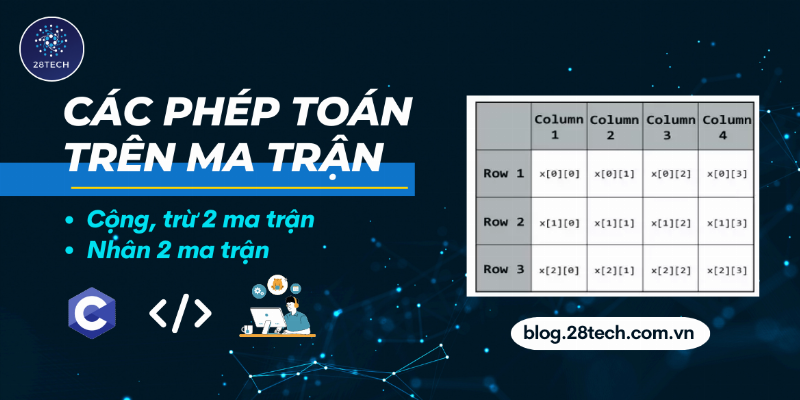
Ma trận và các phép toán: Nền tảng không thể thiếu

Đây là những viên gạch đầu tiên trong ngôi nhà Đại số Tuyến tính.

Bài tập về ma trận thường xoay quanh việc thực hiện các phép cộng, trừ, nhân ma trận; tìm ma trận chuyển vị; tính lũy thừa ma trận; hay các bài toán liên quan đến ma trận nghịch đảo. Nắm vững phần này là cực kỳ quan trọng, bởi ma trận là công cụ để biểu diễn và giải quyết nhiều vấn đề khác trong môn học.

Định thức và ứng dụng: Con số “quyền năng” của ma trận

Định thức là một con số đặc biệt gắn liền với ma trận vuông, mang nhiều ý nghĩa quan trọng.

Các bài tập về định thức bao gồm: tính định thức bằng các phương pháp khác nhau (sarrus, khai triển theo dòng/cột, biến đổi sơ cấp), sử dụng định thức để kiểm tra tính khả nghịch của ma trận, giải hệ phương trình bằng quy tắc Cramer, hay ứng dụng trong hình học (tính diện tích, thể tích).

Hạng ma trận và hệ phương trình tuyến tính: Tìm lời giải cho nhiều ẩn số

Đây là một trong những ứng dụng thực tế và quan trọng nhất của Đại số Tuyến tính.

Bài tập thường yêu cầu: tìm hạng ma trận bằng cách đưa về dạng bậc thang, sử dụng hạng ma trận để biện luận số nghiệm của hệ phương trình tuyến tính, hoặc trực tiếp giải hệ phương trình bằng phương pháp Gauss (khử Gauss) hoặc Gauss-Jordan. Việc thành thạo giải hệ phương trình tuyến tính là kỹ năng cốt lõi cần có.

Không gian vector và cơ sở: Xây dựng “tọa độ” cho thế giới trừu tượng

Khái niệm không gian vector mở ra một thế giới trừu tượng nhưng cực kỳ mạnh mẽ.

Các bài tập trong phần này bao gồm: kiểm tra xem một tập hợp có phải là không gian vector con hay không, kiểm tra tính độc lập tuyến tính của một hệ vector, tìm cơ sở và chiều của không gian vector (hoặc không gian con), tìm tọa độ của một vector đối với một cơ sở cho trước, hay mở rộng một hệ vector độc lập tuyến tính thành một cơ sở.

Ánh xạ tuyến tính: “Biến hình” các vector một cách có quy luật

Ánh xạ tuyến tính mô tả sự “biến đổi” các vector từ không gian này sang không gian khác một cách có cấu trúc tuyến tính.

Bài tập thường yêu cầu: kiểm tra xem một ánh xạ có phải là tuyến tính hay không, tìm ma trận biểu diễn của ánh xạ tuyến tính đối với cặp cơ sở cho trước, tìm hạt nhân (kernel) và ảnh (image) của ánh xạ, xác định tính đơn ánh, toàn ánh, đẳng cấu của ánh xạ.

Trị riêng, vector riêng và dạng toàn phương: Khám phá những hướng “bất biến”

Phần này thường được xem là khó nhất, nhưng lại có nhiều ứng dụng sâu rộng.

Bài tập liên quan đến: tìm đa thức đặc trưng, tìm trị riêng (eigenvalues), tìm vector riêng (eigenvectors) ứng với các trị riêng, chéo hóa ma trận (nếu có thể), đưa dạng toàn phương về dạng chính tắc bằng các phương pháp khác nhau (Lagrange, Jacobi, trực giao).

Tìm bài tập đại số tuyến tính có lời giải ở đâu đáng tin cậy?

Nguồn tài liệu là yếu tố then chốt để bạn tiếp cận được bài tập đại số tuyến tính có lời giải chất lượng.

Bạn có thể tìm thấy chúng trong sách giáo khoa chính thống, sách bài tập đi kèm, các giáo trình hoặc tài liệu tham khảo của giảng viên, các website giáo dục uy tín, hoặc các diễn đàn học thuật nơi sinh viên và giáo viên trao đổi bài tập. Điều quan trọng là chọn nguồn có lời giải chính xác và trình bày rõ ràng.

Phương pháp tiếp cận bài tập đại số tuyến tính có lời giải hiệu quả?

Có lời giải không có nghĩa là bạn chỉ việc “chép” hoặc “đọc lướt”.

Cách tiếp cận hiệu quả nhất là: Đầu tiên, hãy tự mình giải bài tập. Dù có khó khăn đến đâu, hãy cố gắng hết sức, vận dụng kiến thức đã học. Chỉ khi nào thực sự bế tắc hoặc đã giải xong và muốn kiểm tra, bạn mới nên xem lời giải. Khi xem lời giải, đừng chỉ nhìn đáp số cuối cùng. Hãy đọc kỹ từng bước, hiểu logic đằng sau mỗi phép biến đổi, mỗi công thức được áp dụng. Đôi khi, một chi tiết nhỏ trong lời giải lại là “nút thắt” giúp bạn vỡ lẽ ra vấn đề.

Đừng chỉ chép lời giải: Thử thách bản thân trước

Chép lời giải mà không hiểu gì cũng giống như xem người khác tập thể thao mà nghĩ mình sẽ khỏe mạnh.

Quá trình suy nghĩ, thử và sai khi tự giải bài tập mới chính là lúc kiến thức được củng cố. Lời giải chỉ nên là công cụ để bạn kiểm tra, học hỏi, hoặc thoát khỏi bế tắc, chứ không phải là “phao cứu sinh” để bạn bỏ qua nỗ lực ban đầu.

Phân tích từng bước trong lời giải: Đi sâu vào chi tiết

Lời giải chi tiết là “kim chỉ nam” giúp bạn đi đúng đường.

Khi xem lời giải, hãy tự hỏi: “Tại sao lại thực hiện bước này?”, “Công thức này đến từ đâu?”, “Còn cách nào khác để giải không?”. Phân tích sâu từng bước sẽ giúp bạn hiểu rõ bản chất vấn đề, không chỉ đơn thuần là học thuộc lòng cách làm cho một dạng bài cụ thể.

Thử lại với bài tập tương tự: Áp dụng kiến thức vừa học

Hiểu lời giải cho một bài tập là tốt, nhưng khả năng áp dụng cho bài khác mới là mục tiêu cuối cùng.

Sau khi đã hiểu rõ lời giải của một bài, hãy tìm một bài tập khác có dạng tương tự (chỉ thay đổi số liệu hoặc một vài điều kiện nhỏ) và thử tự giải lại từ đầu. Nếu bạn giải được bài mới này, điều đó chứng tỏ bạn đã thực sự nắm vững phương pháp.

Hỏi khi bế tắc: Đừng ngại tìm sự giúp đỡ

Đại số Tuyến tính có những khái niệm khá trừu tượng, việc bế tắc là điều bình thường.

Nếu đã cố gắng hết sức mà vẫn không hiểu lời giải hoặc không tìm ra cách giải, đừng ngần ngại hỏi thầy cô, bạn bè, hoặc tìm kiếm giải thích ở các nguồn khác. Đôi khi, một lời giải thích khác, một góc nhìn khác lại giúp bạn “thông” ngay lập tức.

Cùng đi sâu vào một số bài tập đại số tuyến tính có lời giải tiêu biểu

Để minh họa rõ hơn, chúng ta sẽ cùng xem xét cách tiếp cận một vài dạng bài tập đại số tuyến tính có lời giải phổ biến. Xin lưu ý, đây chỉ là mô tả quy trình giải, không phải lời giải toán học đầy đủ ký hiệu, nhằm giúp bạn hình dung cách “đọc” hiểu một lời giải.

Ví dụ 1: Tìm ma trận nghịch đảo của ma trận cấp 2×2

Bài toán: Tìm ma trận nghịch đảo (nếu có) của ma trận $A = begin{pmatrix} a & b c & d end{pmatrix}$.

Quy trình giải (và cách đọc lời giải):

1. Bước 1: Tính định thức của ma trận A. (Lời giải sẽ hiển thị công thức: det(A) = ad – bc và tính toán cụ thể với số liệu bài cho). Tại sao lại tính định thức? Vì điều kiện cần và đủ để ma trận vuông có ma trận nghịch đảo là định thức của nó phải khác 0. Lời giải chi tiết sẽ giải thích rõ điều này hoặc ngầm hiểu bạn đã nắm vững lý thuyết.
2. Bước 2: Kiểm tra điều kiện khả nghịch. (Lời giải sẽ so sánh det(A) với 0). Nếu det(A) = 0, lời giải sẽ kết luận ma trận A không có ma trận nghịch đảo và dừng lại. Nếu det(A) ≠ 0, lời giải sẽ chuyển sang bước tiếp theo. Tương tự như việc xem [ngày đẹp mua xe tháng 9 năm 2023], bạn cần kiểm tra các điều kiện cần thiết (tài chính, thời điểm,…) trước khi đưa ra quyết định cuối cùng; trong toán học, việc kiểm tra điều kiện là bước bắt buộc trước khi thực hiện các phép tính tiếp theo.
3. Bước 3: Áp dụng công thức tìm ma trận nghịch đảo (đối với ma trận 2×2). (Lời giải sẽ hiển thị công thức: $A^{-1} = frac{1}{text{det}(A)} begin{pmatrix} d & -b -c & a end{pmatrix}$ và thay số vào). Cách đọc lời giải ở đây là hiểu rõ vị trí các phần tử a, b, c, d đã được hoán đổi và đổi dấu như thế nào trong ma trận phụ hợp, rồi nhân với nghịch đảo của định thức.
4. Bước 4: Thực hiện phép nhân ma trận với một số vô hướng. (Lời giải sẽ nhân $frac{1}{text{det}(A)}$ vào từng phần tử của ma trận phụ hợp). Kiểm tra lại các phép tính phân số hoặc số thực để đảm bảo không sai sót.
5. Bước 5: Kết luận. (Lời giải đưa ra ma trận nghịch đảo cuối cùng). Để chắc chắn hơn, bạn có thể tự mình thử nhân ma trận A với ma trận nghịch đảo vừa tìm được. Kết quả phải là ma trận đơn vị. Lời giải chi tiết có thể bao gồm bước kiểm tra này hoặc không.

Ví dụ 2: Giải hệ phương trình tuyến tính bằng phương pháp Gauss

Bài toán: Giải hệ phương trình tuyến tính sau:
$x + 2y – z = 5$
$2x – y + 3z = 1$
$3x + 3y + 2z = 6$

Quy trình giải (và cách đọc lời giải):

1. Bước 1: Lập ma trận mở rộng của hệ phương trình. (Lời giải sẽ viết ma trận mở rộng: $begin{pmatrix} 1 & 2 & -1 & | & 5 2 & -1 & 3 & | & 1 3 & 3 & 2 & | & 6 end{pmatrix}$). Đây là bước “phiên dịch” hệ phương trình sang ngôn ngữ ma trận.

2. Bước 2: Sử dụng các phép biến đổi sơ cấp trên dòng để đưa ma trận về dạng bậc thang. (Lời giải sẽ liệt kê các phép biến đổi cụ thể: $d_2 leftarrow d_2 – 2d_1$, $d_3 leftarrow d_3 – 3d_1$, sau đó $d_3 leftarrow d_3 – k cdot d_2$ với k phù hợp, v.v.). Khi đọc lời giải, hãy tập trung vào mục tiêu của từng phép biến đổi: tạo số 0 ở các vị trí dưới đường chéo chính. Lời giải chi tiết sẽ ghi rõ từng phép biến đổi và ma trận sau mỗi bước.

3. Bước 3: Biện luận và tìm nghiệm từ ma trận bậc thang. (Lời giải sẽ nhìn vào ma trận cuối cùng sau khi đưa về dạng bậc thang).

   • Nếu có dòng dạng $(0 0 … 0 | b)$ với $b neq 0$, hệ vô nghiệm.
   • Nếu số ẩn bằng số phương trình không suy biến (số dòng khác không), hệ có nghiệm duy nhất. Lời giải sẽ dùng phép thế ngược từ dưới lên để tìm các ẩn.
   • Nếu số ẩn lớn hơn số phương trình không suy biến, hệ vô số nghiệm. Lời giải sẽ chọn các ẩn tự do và biểu diễn các ẩn còn lại theo chúng.

   Đọc lời giải ở bước này đòi hỏi bạn hiểu mối quan hệ giữa hạng ma trận hệ số, hạng ma trận mở rộng và số ẩn để đưa ra kết luận đúng về nghiệm.

Ví dụ 3: Tìm cơ sở và chiều của không gian vector con

Bài toán: Tìm cơ sở và chiều của không gian vector con $W = {(x, y, z, t) in mathbb{R}^4 mid x – y + 2z – t = 0}$.

Quy trình giải (và cách đọc lời giải):

1. Bước 1: Biểu diễn các vector trong W dưới dạng tổ hợp tuyến tính. (Lời giải sẽ giải phương trình điều kiện: $x = y – 2z + t$. Sau đó viết vector tổng quát: $(x, y, z, t) = (y – 2z + t, y, z, t)$).
2. Bước 2: Tách vector tổng quát theo các biến tự do. (Lời giải sẽ tách: $(y – 2z + t, y, z, t) = y(1, 1, 0, 0) + z(-2, 0, 1, 0) + t(1, 0, 0, 1)$). Các vector $(1, 1, 0, 0)$, $(-2, 0, 1, 0)$, $(1, 0, 0, 1)$ chính là hệ sinh của W.
3. Bước 3: Kiểm tra tính độc lập tuyến tính của hệ sinh. (Lời giải sẽ lập ma trận từ các vector hệ sinh và đưa về dạng bậc thang, hoặc lập phương trình tổ hợp tuyến tính bằng vector không). Nếu hệ vector độc lập tuyến tính, chúng tạo thành cơ sở. Nếu phụ thuộc tuyến tính, lời giải sẽ loại bỏ vector phụ thuộc để có được cơ sở. Đọc lời giải ở đây cần hiểu các phương pháp kiểm tra độc lập tuyến tính (ví dụ: dùng hạng ma trận).
4. Bước 4: Kết luận cơ sở và chiều. (Lời giải sẽ kết luận tập hợp các vector độc lập tuyến tính tìm được là cơ sở của W và số lượng vector trong cơ sở chính là chiều của W).

Ví dụ 4: Tìm trị riêng, vector riêng của ma trận 2×2

Bài toán: Tìm trị riêng và vector riêng của ma trận $A = begin{pmatrix} 2 & 1 1 & 2 end{pmatrix}$.

Quy trình giải (và cách đọc lời giải):

1. Bước 1: Lập phương trình đặc trưng. (Lời giải sẽ tính $text{det}(A – lambda I) = 0$, tức là $text{det}begin{pmatrix} 2-lambda & 1 1 & 2-lambda end{pmatrix} = 0$. Sau đó khai triển định thức để được đa thức đặc trưng theo $lambda$: $(2-lambda)(2-lambda) – 1 cdot 1 = 0$).

2. Bước 2: Giải phương trình đặc trưng để tìm trị riêng. (Lời giải sẽ giải phương trình bậc hai $(lambda – 2)^2 – 1 = 0$, tức là $lambda^2 – 4lambda + 3 = 0$. Tìm nghiệm $lambda_1, lambda_2$). Các nghiệm này chính là các trị riêng.

3. Bước 3: Với mỗi trị riêng, tìm không gian riêng (tức tập hợp các vector riêng). (Lời giải sẽ lấy từng giá trị $lambda$ tìm được, thay vào phương trình ma trận $(A – lambda I)X = 0$, tức là $begin{pmatrix} 2-lambda & 1 1 & 2-lambda end{pmatrix} begin{pmatrix} x y end{pmatrix} = begin{pmatrix} 0 0 end{pmatrix}$). Đây thực chất là giải một hệ phương trình tuyến tính thuần nhất.

4. Bước 4: Giải hệ phương trình thuần nhất. (Lời giải sẽ giải hệ phương trình cho từng giá trị $lambda$. Ví dụ, với $lambda_1$, ta có hệ mới. Lời giải sẽ chỉ ra dạng tổng quát của các nghiệm $(x, y)$, thường phụ thuộc vào một tham số).

5. Bước 5: Tìm cơ sở của không gian riêng. (Từ dạng tổng quát của nghiệm, lời giải sẽ tách ra các vector tạo thành cơ sở cho không gian riêng ứng với trị riêng đó. Ví dụ, nếu nghiệm là $(t, t)$, cơ sở là ${(1, 1)}$). Các vector này (khác vector không) chính là vector riêng ứng với trị riêng tương ứng.

6. Bước 6: Kết luận. (Lời giải liệt kê các trị riêng và tập hợp các vector riêng (hoặc cơ sở của không gian riêng) ứng với mỗi trị riêng).

Việc đi qua từng bước giải một cách cẩn thận, kết hợp với việc đọc hiểu lý do đằng sau mỗi bước, sẽ giúp bạn nắm vững phương pháp giải cho từng dạng bài. Đây chính là sức mạnh của bài tập đại số tuyến tính có lời giải chất lượng.

Những “bẫy” thường gặp khi làm bài tập đại số tuyến tính và cách tránh

Trên con đường chinh phục Đại số Tuyến tính, có những “cái hố” mà nhiều sinh viên dễ sa chân vào. Nhận diện chúng là cách tốt nhất để tránh.

Một trong những lỗi phổ biến nhất là sai sót trong tính toán cơ bản (cộng, trừ, nhân các số âm, phân số). Đại số Tuyến tính thường liên quan đến nhiều phép tính, chỉ cần một sai lầm nhỏ ở bước đầu có thể dẫn đến kết quả sai hoàn toàn ở cuối cùng. Một “bẫy” khác là nhầm lẫn giữa các khái niệm (ví dụ: không gian vector và không gian con, độc lập tuyến tính và phụ thuộc tuyến tính). Việc không nắm vững định nghĩa và điều kiện áp dụng các định lý cũng là nguyên nhân dẫn đến sai lầm.

Cẩn thận với các phép tính đại số

Hãy kiểm tra lại từng phép tính, đặc biệt là khi làm việc với phân số và số âm.

Đôi khi, sử dụng một dòng nháp hoặc làm chậm lại một chút để đảm bảo tính chính xác của các phép nhân, cộng, trừ là hoàn toàn xứng đáng. Nhiều bài bài tập đại số tuyến tính có lời giải chỉ ra đáp số cuối cùng, nhưng bạn cần tự mình kiểm tra lại các bước tính toán trung gian.

Hiểu rõ định nghĩa và định lý

Lý thuyết là kim chỉ nam cho thực hành.

Đừng cố gắng làm bài tập khi chưa hiểu rõ lý thuyết liên quan. Quay trở lại đọc kỹ định nghĩa, định lý, và các ví dụ minh họa trong giáo trình. Hiểu đúng bản chất của các khái niệm như “cơ sở”, “chiều”, “hạng”, “trị riêng” sẽ giúp bạn áp dụng phương pháp giải chính xác. Việc này quan trọng không kém việc nắm vững kiến thức nền tảng cho các môn học khác như [sách triết học mác lênin](), nơi các khái niệm và nguyên lý cũng cần được hiểu sâu sắc để áp dụng vào phân tích.

Nắm vững các phương pháp giải tiêu chuẩn

Mỗi dạng bài thường có một hoặc vài phương pháp giải tiêu chuẩn.

Ví dụ, giải hệ phương trình tuyến tính thường dùng Gauss, Cramer, hoặc ma trận nghịch đảo. Tìm cơ sở và chiều thường liên quan đến việc giải hệ phương trình thuần nhất. Nắm vững quy trình từng bước của các phương pháp này sẽ giúp bạn giải bài tập một cách có hệ thống và hiệu quả. Khi bạn xem bài tập đại số tuyến tính có lời giải, hãy cố gắng nhận diện phương pháp nào đang được áp dụng và tại sao.

Lời khuyên từ chuyên gia để làm chủ Đại số Tuyến tính

Chúng tôi đã trò chuyện với PGS. TS. Lê Văn An, một giảng viên giàu kinh nghiệm về Toán cao cấp, và nhận được lời khuyên quý báu.

Theo ông An: “Nhiều sinh viên xem Đại số Tuyến tính là môn lý thuyết suông, nhưng thực tế nó cực kỳ thực tiễn và logic. Chìa khóa để học tốt không phải là học thuộc lòng công thức, mà là hiểu rõ vì sao công thức đó đúng và khi nào áp dụng. Luyện tập bài tập đại số tuyến tính có lời giải là cách tốt nhất để rèn luyện tư duy logic và khả năng áp dụng kiến thức. Hãy coi lời giải như một người bạn đồng hành, không phải là ‘phao’. Tự làm, tự sai, tự sửa từ lời giải – đó mới là học.”

Lời khuyên của chuyên gia nhấn mạnh tầm quan trọng của việc chủ động học và sử dụng lời giải một cách thông minh.

Kết nối kiến thức Đại số Tuyến tính với thực tế (và báo cáo thực tập!)

Nghe có vẻ khó tin, nhưng Đại số Tuyến tính không chỉ là môn học lý thuyết trên giảng đường. Nó có vô vàn ứng dụng trong đời sống và các lĩnh vực khoa học kỹ thuật hiện đại.

Từ đồ họa máy tính (biến đổi hình ảnh dùng ma trận), xử lý tín hiệu (nén ảnh, âm thanh), kinh tế lượng (mô hình kinh tế), tối ưu hóa, cho đến các thuật toán học máy (machine learning) và khoa học dữ liệu (phân tích dữ liệu lớn), Đại số Tuyến tính đều đóng vai trò nền tảng.

Việc thành thạo các kỹ năng giải bài tập đại số tuyến tính có lời giải không chỉ giúp bạn qua môn, mà còn rèn luyện cho bạn khả năng tư duy phân tích logic, giải quyết vấn đề một cách hệ thống. Những kỹ năng này cực kỳ quan trọng khi bạn đi thực tập và viết [báo cáo tốt nghiệp ngành điều dưỡng](), hay bất kỳ ngành nào khác. Dù ngành nghề có vẻ không liên quan trực tiếp đến toán, khả năng xử lý thông tin, phân tích dữ liệu (dưới dạng bảng, biểu đồ – thường được xây dựng từ dữ liệu có cấu trúc ma trận), và trình bày vấn đề một cách logic là kỹ năng chung mà mọi nhà tuyển dụng đều tìm kiếm.

Thậm chí, việc lập kế hoạch và cấu trúc một báo cáo hay một đề án, như [đề án thành lập trung tâm ngoại ngữ](), đòi hỏi bạn phải phân tích các yếu tố, sắp xếp chúng theo một trật tự logic, và đánh giá tác động qua lại giữa các phần – một quá trình tư duy có nhiều điểm tương đồng với việc phân tích mối quan hệ giữa các biến trong hệ phương trình hay cấu trúc của không gian vector.

Việc luyện tập giải bài tập đại số tuyến tính có lời giải chính là bạn đang đầu tư vào khả năng tư duy phản biện và giải quyết vấn đề của mình, những kỹ năng không chỉ hữu ích cho môn học mà còn cho sự nghiệp sau này.

Lời kết

Đại số Tuyến tính có thể là một thử thách, nhưng nó là thử thách xứng đáng để vượt qua. Với sự kiên trì và phương pháp học đúng đắn, bạn hoàn toàn có thể làm chủ môn học này. Bài tập đại số tuyến tính có lời giải chính là công cụ đắc lực giúp bạn trên hành trình đó. Chúng cung cấp cho bạn cơ hội thực hành, kiểm tra kiến thức, và học hỏi từ những sai lầm trong một môi trường an toàn.

Hãy bắt đầu ngay hôm nay! Tìm kiếm những nguồn bài tập đại số tuyến tính có lời giải đáng tin cậy, bắt tay vào giải, và sử dụng lời giải một cách thông minh để nâng cao hiểu biết của mình. Nhớ rằng, “Trăm hay không bằng tay quen” – thực hành càng nhiều, bạn càng thành thạo. Baocaothuctap.net hy vọng bài viết này đã cung cấp cho bạn cái nhìn rõ ràng hơn về tầm quan trọng và cách sử dụng hiệu quả bài tập có lời giải trong môn Đại số Tuyến tính. Chúc bạn học tốt và thành công!