Giải Ngay Bài Tập Phân Phối Chuẩn: Hướng Dẫn Chi Tiết Từ A-Z

Thống kê, nghe qua có vẻ khô khan và đầy những con số, công thức khó hiểu. Nhưng thực tế, nó lại là “người bạn” đắc lực giúp chúng ta hiểu rõ hơn về thế giới xung quanh, từ kết quả học tập của học sinh, chiều cao trung bình của người Việt, cho đến dự đoán xu hướng thị trường hay kiểm soát chất lượng sản phẩm. Và nhắc đến thống kê, không thể không nhắc đến “phân phối chuẩn” – một trong những khái niệm “quốc dân”, xuất hiện “như cơm bữa” trong rất nhiều lĩnh vực. Tuy nhiên, việc làm quen và giải quyết các Bài Tập Phân Phối Chuẩn lại khiến không ít người “đau đầu vắt óc”. Bạn có từng thấy những biểu đồ hình chuông quen thuộc trên sách vở hay báo cáo chưa? Đó chính là hình ảnh đại diện của phân phối chuẩn đấy!

Chào mừng bạn đến với Baocaothuctap.net, nơi chúng ta sẽ cùng nhau “giải mã” những khái niệm phức tạp thành những kiến thức dễ hiểu, dễ áp dụng. Hôm nay, chúng ta sẽ cùng nhau “lật tung” mọi ngóc ngách liên quan đến các bài tập phân phối chuẩn, từ lý thuyết đến thực hành, giúp bạn tự tin “cân” mọi dạng bài. Dù bạn đang chuẩn bị báo cáo thực tập có sử dụng số liệu thống kê, hay đơn giản là muốn nâng cao kiến thức về lĩnh vực này, bài viết này chắc chắn sẽ mang lại nhiều giá trị. Tương tự như việc tìm hiểu cách [đọc kết quả đo chức năng hô hấp] để hiểu tình trạng sức khỏe, việc nắm vững phân phối chuẩn sẽ giúp bạn “đọc” được dữ liệu hiệu quả hơn nhiều.

Phân Phối Chuẩn Là Gì Mà Quan Trọng Đến Thế?

Phân phối chuẩn: “Ngôi sao” của thế giới thống kê là gì?

Phân phối chuẩn, hay còn gọi là phân phối Gaussian, là một loại phân phối xác suất liên tục. Nghe thuật ngữ có vẻ hàn lâm, nhưng hình dung đơn giản nhất về phân phối chuẩn chính là đồ thị hình “chuông” đối xứng. Điểm cao nhất của chuông nằm ở trung bình, và hai “cánh” chuông trải đều sang hai bên, càng xa trung bình thì độ cao (tức tần suất xuất hiện) càng giảm dần.

Tại sao phân phối chuẩn lại “phủ sóng” rộng khắp?

Câu hỏi này thú vị đấy! Phân phối chuẩn xuất hiện tự nhiên trong rất nhiều hiện tượng thực tế. Chiều cao, cân nặng của một nhóm người; điểm thi của một lớp học đông; sai số khi đo lường; tuổi thọ của một loại bóng đèn; hay thậm chí là giá cổ phiếu thay đổi hàng ngày… Rất nhiều dữ liệu thu thập được trong tự nhiên và xã hội có xu hướng tuân theo phân phối chuẩn, hoặc ít nhất là xấp xỉ phân phối chuẩn. Điều này là do Định lý Giới hạn Trung tâm (Central Limit Theorem) nổi tiếng trong thống kê – một “bảo bối” cho thấy trung bình của các mẫu lớn được lấy từ bất kỳ phân phối nào (miễn là có phương sai hữu hạn) sẽ xấp xỉ phân phối chuẩn. Nhờ đó, phân phối chuẩn trở thành công cụ mạnh mẽ để mô hình hóa, phân tích và đưa ra dự đoán về các tập dữ liệu lớn.

Nắm Vững Công Cụ: Trung Bình, Độ Lệch Chuẩn Và Giá Trị Z

Trước khi “nhảy” vào giải bài tập phân phối chuẩn, chúng ta cần làm quen với hai tham số “sinh đôi” quyết định hình dạng của chuông phân phối chuẩn và một “anh chàng” giúp chúng ta làm việc với bảng thống kê.

Trung bình (μ): Trái tim của phân phối chuẩn

Trung bình (ký hiệu là μ – đọc là “muy” đối với tổng thể, hoặc x̄ – đọc là “x gạch” đối với mẫu) là giá trị trung tâm của phân phối. Nó nằm ngay đỉnh của đồ thị hình chuông và chia phân phối thành hai phần đối xứng hoàn hảo. Trung bình cho chúng ta biết “điểm giữa” hay giá trị điển hình của tập dữ liệu.

Độ lệch chuẩn (σ): “Độ gầy, béo” của chuông

Độ lệch chuẩn (ký hiệu là σ – đọc là “sigma” đối với tổng thể, hoặc s đối với mẫu) đo lường mức độ phân tán hay “độ rộng” của dữ liệu xung quanh giá trị trung bình.

• Độ lệch chuẩn nhỏ: Dữ liệu tập trung sát trung bình, đồ thị chuông cao và “gầy”.
• Độ lệch chuẩn lớn: Dữ liệu phân tán xa trung bình, đồ thị chuông thấp và “béo”.

Độ lệch chuẩn là “chìa khóa” để hiểu dữ liệu lan rộng đến đâu. Ví dụ, hai lớp học có cùng điểm trung bình 7.0, nhưng lớp A có độ lệch chuẩn 1.0 (điểm đa số tập trung từ 6.0 đến 8.0), còn lớp B có độ lệch chuẩn 2.5 (điểm phân tán rộng từ 4.5 đến 9.5). Điều này cho thấy dù trung bình như nhau, nhưng sự phân bố điểm ở hai lớp lại rất khác biệt.

Giá trị Z (Z-score): “Cây cầu” nối dữ liệu thô với bảng thống kê

Đây là một khái niệm cực kỳ quan trọng khi giải bài tập phân phối chuẩn. Giá trị Z, hay còn gọi là điểm Z, cho chúng ta biết một giá trị dữ liệu X cụ thể nằm cách trung bình bao nhiêu độ lệch chuẩn.
Công thức tính giá trị Z là:

Z = (X – μ) / σ

Trong đó:

• X: Giá trị dữ liệu cụ thể mà bạn muốn tìm điểm Z.
• μ: Giá trị trung bình của phân phối.
• σ: Độ lệch chuẩn của phân phối.

Giá trị Z có ý nghĩa rất lớn. Một giá trị Z dương nghĩa là X nằm trên trung bình. Một giá trị Z âm nghĩa là X nằm dưới trung bình. Giá trị Z bằng 0 nghĩa là X chính bằng trung bình. Giá trị tuyệt đối của Z càng lớn, nghĩa là X càng nằm xa trung bình.

Điều kỳ diệu của giá trị Z là nó “chuẩn hóa” mọi phân phối chuẩn về cùng một “sân chơi” – đó là phân phối chuẩn tắc (Standard Normal Distribution), với trung bình bằng 0 và độ lệch chuẩn bằng 1. Điều này cho phép chúng ta sử dụng Bảng Z (Z-table) để tìm xác suất tương ứng với bất kỳ giá trị Z nào. Bảng Z là công cụ không thể thiếu khi bạn giải các bài tập phân phối chuẩn liên quan đến xác suất.

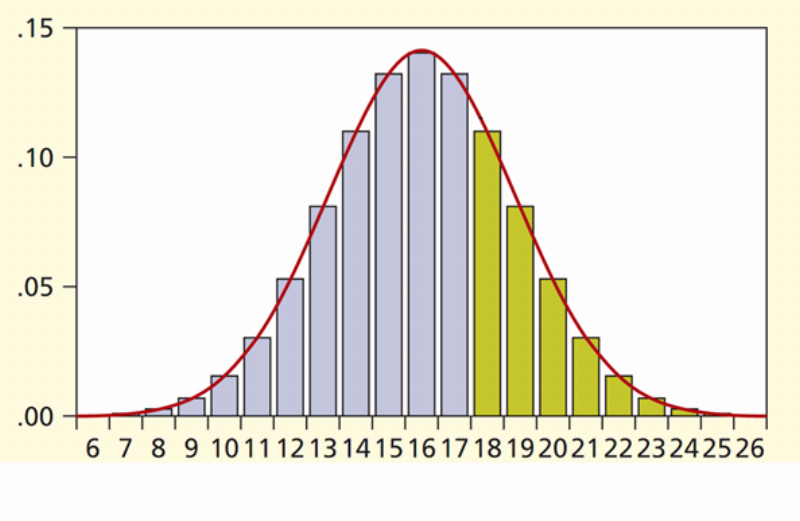Công thức tính giá trị Z trong phân phối chuẩn tắc

Các Dạng Bài Tập Phân Phối Chuẩn Thường Gặp

Khi làm bài tập phân phối chuẩn, bạn sẽ thường xuyên đối mặt với những dạng câu hỏi sau:

1. Tìm xác suất khi biết giá trị X

Đây là dạng bài phổ biến nhất. Bạn được cho trung bình (μ), độ lệch chuẩn (σ) của một phân phối chuẩn và một giá trị X cụ thể. Yêu cầu là tính xác suất để một giá trị ngẫu nhiên được chọn từ phân phối đó nhỏ hơn X, lớn hơn X, hoặc nằm giữa hai giá trị X1 và X2.

• P(X < x): Xác suất để giá trị nhỏ hơn x.
• P(X > x): Xác suất để giá trị lớn hơn x.
• P(x1 < X < x2): Xác suất để giá trị nằm giữa x1 và x2.

2. Tìm giá trị X khi biết xác suất

Ngược lại với dạng 1, bạn được cho trung bình, độ lệch chuẩn và một xác suất (ví dụ: 10% giá trị thấp nhất, 5% giá trị cao nhất, hoặc giá trị mà 75% dữ liệu nhỏ hơn nó). Yêu cầu là tìm giá trị X tương ứng với xác suất đó. Dạng này đòi hỏi bạn phải “đọc ngược” Bảng Z.

3. Bài toán liên quan đến mẫu

Đây là dạng nâng cao hơn, liên quan đến phân phối của trung bình mẫu. Theo Định lý Giới hạn Trung tâm, nếu kích thước mẫu đủ lớn (thường n > 30), thì phân phối của trung bình mẫu (x̄) sẽ xấp xỉ phân phối chuẩn, với trung bình bằng μ của tổng thể và độ lệch chuẩn bằng σ/√n (gọi là sai số chuẩn của trung bình). Bạn sẽ phải tính xác suất cho trung bình của một mẫu, hoặc tìm giá trị trung bình mẫu tương ứng với một xác suất cho trước. Công thức tính giá trị Z cho trung bình mẫu sẽ là:

Z = (x̄ – μ) / (σ/√n)

Việc làm quen với nhiều dạng bài tập phân phối chuẩn sẽ giúp bạn rèn luyện kỹ năng và tư duy giải quyết vấn đề. Tương tự như việc luyện giải [bài tập kế toán tài chính 3 có đáp an] để thành thạo nghiệp vụ, càng thực hành nhiều với phân phối chuẩn, bạn càng dễ dàng nắm bắt bản chất và áp dụng linh hoạt.

Hướng Dẫn “Giải Vèo Vèo” Bài Tập Phân Phối Chuẩn

Đừng lo nếu bạn cảm thấy mơ hồ ban đầu. Chúng ta sẽ đi từng bước một để “thuần phục” các bài tập phân phối chuẩn.

Bước 1: Xác định thông tin “đề bài cho” và “đề bài hỏi”

Đọc kỹ đề bài để xác định các giá trị đã biết:

• Trung bình (μ) của tổng thể.
• Độ lệch chuẩn (σ) của tổng thể.
• Giá trị X cụ thể (hoặc các giá trị X1, X2) hoặc xác suất P.
• Đối với bài toán về mẫu, cần biết thêm kích thước mẫu (n).

Xác định rõ yêu cầu của đề bài:

• Tính xác suất P(X < x), P(X > x), P(x1 < X < x2)?
• Tìm giá trị X tương ứng với một xác suất P cho trước?
• Tính xác suất P(x̄ < x̄₀), P(x̄ > x̄₀), P(x̄₁ < x̄ < x̄₂)?
• Tìm giá trị trung bình mẫu x̄ tương ứng với một xác suất P cho trước?

Việc này nghe đơn giản nhưng cực kỳ quan trọng, giúp bạn định hình phương pháp giải.

Bước 2: Chuyển giá trị X về giá trị Z (Chuẩn hóa)

Đây là bước “chuẩn hóa” dữ liệu của bạn về phân phối chuẩn tắc (μ=0, σ=1) để có thể sử dụng Bảng Z.

• Nếu đề bài hỏi về giá trị X đơn lẻ: Sử dụng công thức Z = (X – μ) / σ
• Nếu đề bài hỏi về trung bình mẫu x̄: Sử dụng công thức Z = (x̄ – μ) / (σ/√n)

Luôn nhớ rằng giá trị Z biểu thị số lượng độ lệch chuẩn mà giá trị X (hoặc x̄) cách trung bình.

Bước 3: Sử dụng Bảng Z để tìm xác suất hoặc giá trị Z tương ứng

Bảng Z là công cụ chính ở bước này.

• Nếu bạn có Z và cần tìm xác suất: Tìm giá trị Z của bạn trong bảng. Bảng Z thường cho xác suất P(Z < z), tức là diện tích dưới đường cong chuẩn tắc từ -∞ đến z.
  • Để tìm P(X < x) -> tìm P(Z < z) trực tiếp từ bảng.
  • Để tìm P(X > x) -> tìm P(Z > z) = 1 – P(Z < z).
  • Để tìm P(x1 < X < x2) -> chuyển cả x1 và x2 sang Z1 và Z2. Tính P(Z1 < Z < Z2) = P(Z < Z2) – P(Z < Z1).
  • Chú ý bảng Z của bạn thể hiện diện tích ở đâu (bên trái Z, bên phải Z, hay ở giữa 0 và Z) để sử dụng công thức phù hợp. Hầu hết các bảng chuẩn phổ biến đều cho P(Z < z).
• Nếu bạn có xác suất và cần tìm Z: Tìm xác suất P trong phần thân của Bảng Z. Sau đó, “đọc ngược” ra giá trị Z tương ứng ở hàng và cột viền của bảng.

Bước 4: Diễn giải kết quả

Kết quả từ Bảng Z là một xác suất (giá trị từ 0 đến 1). Hãy diễn giải con số này trong ngữ cảnh của bài toán gốc. Ví dụ: “Xác suất để chiều cao của một người ngẫu nhiên nhỏ hơn 165cm là 0.25” (hoặc 25%).

Nếu bạn cần tìm giá trị X từ xác suất, sau khi tìm được Z từ bảng, hãy sử dụng công thức Z đảo ngược để tìm X:

X = μ + Z * σ

Hoặc, đối với trung bình mẫu:

x̄ = μ + Z * (σ/√n)

Ví dụ minh họa: “Giải ngố” bài tập cụ thể

Giả sử chiều cao của nam thanh niên Việt Nam tuân theo phân phối chuẩn với trung bình μ = 168 cm và độ lệch chuẩn σ = 5 cm.

Bài tập 1: Tính xác suất để một nam thanh niên ngẫu nhiên có chiều cao nhỏ hơn 175 cm.

• Bước 1: Biết μ=168, σ=5, X=175. Cần tính P(X < 175).
• Bước 2: Chuyển X về Z: Z = (175 – 168) / 5 = 7 / 5 = 1.4.
• Bước 3: Tìm P(Z < 1.4) trong Bảng Z. Giả sử tra bảng ta được P(Z < 1.4) ≈ 0.9192.
• Bước 4: Diễn giải: Xác suất để một nam thanh niên ngẫu nhiên có chiều cao nhỏ hơn 175 cm là khoảng 0.9192, hay 91.92%.

Bài tập 2: Tính xác suất để một nam thanh niên ngẫu nhiên có chiều cao lớn hơn 160 cm.

• Bước 1: Biết μ=168, σ=5, X=160. Cần tính P(X > 160).
• Bước 2: Chuyển X về Z: Z = (160 – 168) / 5 = -8 / 5 = -1.6.
• Bước 3: Tìm P(Z < -1.6) trong Bảng Z. Do tính đối xứng, P(Z < -1.6) = P(Z > 1.6). Tra bảng P(Z < 1.6) ≈ 0.9452. Vậy P(Z > 1.6) = 1 – 0.9452 = 0.0548. Do đó, P(Z < -1.6) ≈ 0.0548.
  • Chúng ta cần tính P(X > 160), tương ứng với P(Z > -1.6). P(Z > -1.6) = 1 – P(Z < -1.6) = 1 – 0.0548 = 0.9452. (Hoặc đơn giản hơn, do tính đối xứng, P(Z > -1.6) = P(Z < 1.6) ≈ 0.9452).
• Bước 4: Diễn giải: Xác suất để một nam thanh niên ngẫu nhiên có chiều cao lớn hơn 160 cm là khoảng 0.9452, hay 94.52%.

Bài tập 3: Khoảng chiều cao nào chứa 90% nam thanh niên ở trung tâm phân phối?

• Bước 1: Biết μ=168, σ=5. Cần tìm khoảng (x1, x2) sao cho P(x1 < X < x2) = 0.90 và khoảng này đối xứng qua trung bình. Điều này có nghĩa là diện tích ở hai đuôi phân phối (nhỏ hơn x1 và lớn hơn x2) mỗi bên là (1 – 0.90) / 2 = 0.05.
• Bước 2: Tìm giá trị Z tương ứng với xác suất tích lũy (diện tích từ -∞) là 0.05 và 0.95.
  • Tìm Z1 sao cho P(Z < Z1) = 0.05. Tra Bảng Z ngược, tìm giá trị gần 0.05 nhất trong thân bảng. Ta sẽ tìm được Z1 ≈ -1.645.
  • Tìm Z2 sao cho P(Z < Z2) = 0.95. Tra Bảng Z ngược, tìm giá trị gần 0.95 nhất trong thân bảng. Ta sẽ tìm được Z2 ≈ 1.645. (Đúng như mong đợi, Z2 = -Z1 do tính đối xứng).
• Bước 3: Chuyển Z1, Z2 về X1, X2.
  • X1 = μ + Z1 σ = 168 + (-1.645) 5 = 168 – 8.225 = 159.775 cm.
  • X2 = μ + Z2 σ = 168 + (1.645) 5 = 168 + 8.225 = 176.225 cm.
• Bước 4: Diễn giải: 90% nam thanh niên Việt Nam có chiều cao nằm trong khoảng từ 159.775 cm đến 176.225 cm.

Đây chỉ là ba ví dụ cơ bản nhất. Các bài tập phân phối chuẩn có thể phức tạp hơn khi kết hợp nhiều yêu cầu hoặc liên quan đến so sánh giữa các nhóm. Tuy nhiên, “xương sống” của phương pháp giải vẫn là chuyển về Z và sử dụng Bảng Z (hoặc các công cụ tính toán khác).

Để giải quyết các bài tập định lượng một cách bài bản và hiệu quả, không chỉ riêng thống kê mà còn trong nhiều lĩnh vực khác như kinh tế, kỹ thuật, việc có nguồn tài liệu và bài tập mẫu là cực kỳ cần thiết. Nếu bạn đang tìm kiếm tài liệu ôn tập hay các bài tập thực hành, những nguồn như [bài tập vật liệu xây dựng] hoặc các bài tập chuyên ngành khác trên Baocaothuctap.net có thể là điểm khởi đầu tốt để bạn rèn luyện kỹ năng giải quyết vấn đề.

Ứng Dụng Thực Tế Của Phân Phối Chuẩn (Vượt Ra Ngoài Bài Tập)

Tại sao chúng ta phải “vật lộn” với các bài tập phân phối chuẩn? Đơn giản vì nó là nền tảng cho rất nhiều ứng dụng quan trọng trong cuộc sống và công việc.

Trong Nghiên Cứu Khoa Học và Xã Hội

Phân phối chuẩn được sử dụng rộng rãi để mô tả các đặc điểm của quần thể, phân tích kết quả khảo sát, kiểm định giả thuyết thống kê. Khi bạn đọc một nghiên cứu về ảnh hưởng của một phương pháp giảng dạy mới lên điểm thi của học sinh, khả năng rất cao dữ liệu điểm thi được giả định tuân theo phân phối chuẩn để áp dụng các phương pháp kiểm định như kiểm định t (t-test) hay kiểm định F (ANOVA).

Trong Kinh Doanh và Marketing

Các nhà phân tích kinh doanh sử dụng phân phối chuẩn để mô hình hóa biến động giá cổ phiếu, dự báo doanh số bán hàng, phân tích rủi ro tài chính. Trong marketing, nó giúp hiểu rõ sự phân bố của các đặc điểm khách hàng (tuổi, thu nhập), từ đó định hình chiến lược quảng cáo hiệu quả hơn. Chẳng hạn, nếu một công ty muốn nhắm mục tiêu đến nhóm khách hàng có thu nhập trung bình, việc biết phân phối thu nhập của thị trường sẽ giúp họ xác định đúng phân khúc. Khi lập [đề tài báo cáo thực tập marketing], việc phân tích dữ liệu khách hàng bằng các công cụ thống kê, bao gồm cả phân phối chuẩn, sẽ làm tăng tính thuyết phục và chuyên nghiệp cho báo cáo của bạn.

Biểu đồ thể hiện ứng dụng phân phối chuẩn trong phân tích dữ liệu marketing

Trong Kiểm Soát Chất Lượng

Trong sản xuất, phân phối chuẩn giúp kiểm tra xem sản phẩm có đạt tiêu chuẩn chất lượng hay không. Kích thước, trọng lượng, độ bền của sản phẩm thường tuân theo phân phối chuẩn. Bằng cách tính xác suất sản phẩm nằm ngoài giới hạn cho phép, nhà sản xuất có thể điều chỉnh quy trình để giảm thiểu sản phẩm lỗi.

Trong Y Học

Trong y học, phân phối chuẩn được sử dụng để thiết lập phạm vi “bình thường” cho các chỉ số sức khỏe như huyết áp, mức cholesterol, kết quả xét nghiệm máu. Bác sĩ dựa vào đó để đánh giá tình trạng sức khỏe của bệnh nhân.

Như bạn thấy đấy, việc thành thạo bài tập phân phối chuẩn không chỉ giúp bạn vượt qua các kỳ thi hay hoàn thành báo cáo, mà còn mở ra cánh cửa để hiểu và ứng dụng thống kê vào rất nhiều lĩnh vực khác nhau trong cuộc sống và sự nghiệp.

Lời Khuyên Từ Chuyên Gia Giả Định

“Theo kinh nghiệm của tôi sau nhiều năm làm việc với dữ liệu,” – Tiến sĩ Nguyễn Thị Mai, chuyên gia phân tích dữ liệu tại một viện nghiên cứu uy tín chia sẻ – “điểm mấu chốt khi làm bài tập phân phối chuẩn không chỉ là nhớ công thức hay cách tra bảng, mà là hiểu được ý nghĩa đằng sau con số. Hãy luôn tự hỏi: Giá trị Z này nói lên điều gì về vị trí của dữ liệu? Xác suất này có ý nghĩa gì trong ngữ cảnh bài toán thực tế? Việc đặt câu hỏi và tìm câu trả lời sẽ giúp bạn nắm vững kiến thức một cách sâu sắc hơn rất nhiều.”

Lời khuyên này thật chí lý phải không? Đừng chỉ giải bài tập một cách máy móc. Hãy cố gắng hình dung đồ thị, ý nghĩa của trung bình và độ lệch chuẩn, và xác suất mà bạn đang tính toán.

Những “Cạm Bẫy” Cần Tránh Khi Giải Bài Tập Phân Phối Chuẩn

Dù đã nắm vững các bước, bạn vẫn có thể gặp phải một vài lỗi phổ biến:

• Nhầm lẫn Bảng Z: Một số Bảng Z cho xác suất P(Z < z), một số cho P(0 < Z < z), một số lại cho P(Z > z). Luôn kiểm tra kỹ loại Bảng Z bạn đang dùng và điều chỉnh công thức tính xác suất cho phù hợp (ví dụ: P(Z > z) = 1 – P(Z < z) nếu bảng cho P(Z < z)).
• Tính sai giá trị Z: Sai sót trong phép tính cộng, trừ, nhân, chia khi tính Z là điều thường gặp. Hãy kiểm tra lại các bước tính toán của bạn.
• Không chuẩn hóa đơn vị: Đảm bảo giá trị X, trung bình và độ lệch chuẩn có cùng đơn vị trước khi tính Z.
• Quên chia cho √n trong bài toán mẫu: Đây là lỗi rất phổ biến khi làm bài tập liên quan đến trung bình mẫu. Nhớ rằng sai số chuẩn của trung bình mẫu là σ/√n.
• Diễn giải sai kết quả: Kết quả là xác suất (từ 0 đến 1). Đừng nhầm lẫn nó với giá trị dữ liệu hay tỷ lệ phần trăm (trừ khi bạn nhân với 100%).

Thực Hành Là Chìa Khóa

Lý thuyết chỉ là “bản đồ”. Để “thám hiểm” và làm chủ vùng đất phân phối chuẩn, bạn cần phải thực hành. Hãy tìm kiếm thêm các bài tập phân phối chuẩn từ sách giáo khoa, các nguồn trực tuyến, hoặc đề thi cũ. Bắt đầu từ những bài cơ bản, sau đó nâng dần độ khó. Đừng ngại mắc lỗi, mỗi lỗi sai là một cơ hội để học hỏi.

Bạn có thể tự đặt ra các bài tập nhỏ dựa trên các tình huống thực tế xung quanh mình. Ví dụ: “Giả sử thời gian bạn hoàn thành báo cáo thực tập tuân theo phân phối chuẩn với trung bình X ngày và độ lệch chuẩn Y ngày. Tính xác suất để bạn hoàn thành báo cáo trong vòng Z ngày?” Việc liên hệ với thực tế sẽ giúp bạn thấy môn thống kê không còn khô khan nữa.

Nhớ rằng, mục tiêu của việc giải bài tập phân phối chuẩn không chỉ là ra được đáp số đúng, mà quan trọng hơn là hiểu được ý nghĩa của phân phối chuẩn và cách áp dụng nó để phân tích dữ liệu trong nhiều tình huống khác nhau.

Tổng Kết

Chúng ta đã cùng nhau đi qua một hành trình khám phá về bài tập phân phối chuẩn, từ những khái niệm cơ bản nhất về phân phối chuẩn, trung bình, độ lệch chuẩn, giá trị Z, cho đến các dạng bài thường gặp, hướng dẫn giải chi tiết từng bước, và cả những ứng dụng thực tế của nó. Phân phối chuẩn không chỉ là một khái niệm lý thuyết, mà là một công cụ mạnh mẽ giúp chúng ta hiểu và xử lý dữ liệu trong thế giới thực.

Giải bài tập phân phối chuẩn đòi hỏi sự kiên nhẫn, cẩn thận và hiểu biết về các khái niệm cốt lõi cùng với cách sử dụng Bảng Z. Tuy nhiên, với hướng dẫn chi tiết và các ví dụ minh họa mà chúng tôi đã cung cấp, hy vọng bạn đã cảm thấy tự tin hơn rất nhiều.

Đừng ngần ngại bắt tay vào thực hành ngay từ bây giờ! Càng làm nhiều bài tập phân phối chuẩn, bạn sẽ càng thành thạo. Hãy xem đây là một kỹ năng đầu tư cho tương lai của bạn, dù bạn theo đuổi ngành nghề nào. Chúc bạn thành công trên con đường chinh phục môn thống kê và các bài tập phân phối chuẩn đầy thử thách nhưng cũng rất thú vị này!