Bạn đang tìm kiếm tài liệu về bài tập tương quan và hồi quy có đáp án để củng cố kiến thức và chuẩn bị cho bài kiểm tra sắp tới? Hay bạn đang gặp khó khăn trong việc hiểu và áp dụng các khái niệm thống kê này vào thực tiễn? Đừng lo lắng, bài viết này sẽ là người bạn đồng hành đáng tin cậy của bạn, cung cấp hướng dẫn chi tiết, đầy đủ các ví dụ minh họa và đặc biệt là những bài bài tập tương quan và hồi quy có đáp án để bạn tự luyện tập và đánh giá năng lực bản thân. Chúng ta sẽ cùng nhau khám phá thế giới thú vị của tương quan và hồi quy, từ những khái niệm cơ bản đến những ứng dụng thực tiễn.
Mục Lục
Hiểu rõ về tương quan: Mối liên hệ giữa các biến số
Trước khi bước vào phần thực hành với các bài tập tương quan và hồi quy có đáp án, hãy cùng làm rõ khái niệm tương quan. Tương quan là gì? Nói một cách đơn giản, đó là mối liên hệ giữa hai hay nhiều biến số. Ví dụ, bạn có nhận thấy rằng khi thời tiết càng nóng, lượng nước bạn uống càng tăng? Đây chính là một ví dụ về tương quan dương: khi một biến tăng, biến kia cũng tăng theo. Ngược lại, nếu bạn nhận thấy khi lượng cafein tiêu thụ càng nhiều thì chất lượng giấc ngủ càng giảm, đó là tương quan âm.
Phân loại các loại tương quan
Chúng ta có thể phân loại tương quan dựa trên hướng và độ mạnh yếu:
- Tương quan dương: Hai biến cùng chiều biến thiên. Càng nhiều nắng, cây càng phát triển tốt.
- Tương quan âm: Hai biến ngược chiều biến thiên. Càng học ít, điểm thi càng thấp.
- Tương quan không: Hai biến không có mối liên hệ rõ ràng. Màu mắt và chiều cao.
Độ mạnh yếu của tương quan được đo bằng hệ số tương quan, thường là hệ số tương quan Pearson (r), có giá trị từ -1 đến +1.
- r = +1: Tương quan dương hoàn hảo.
- r = -1: Tương quan âm hoàn hảo.
- r = 0: Không có tương quan tuyến tính.
Khám phá hồi quy: Dự đoán giá trị biến số phụ thuộc
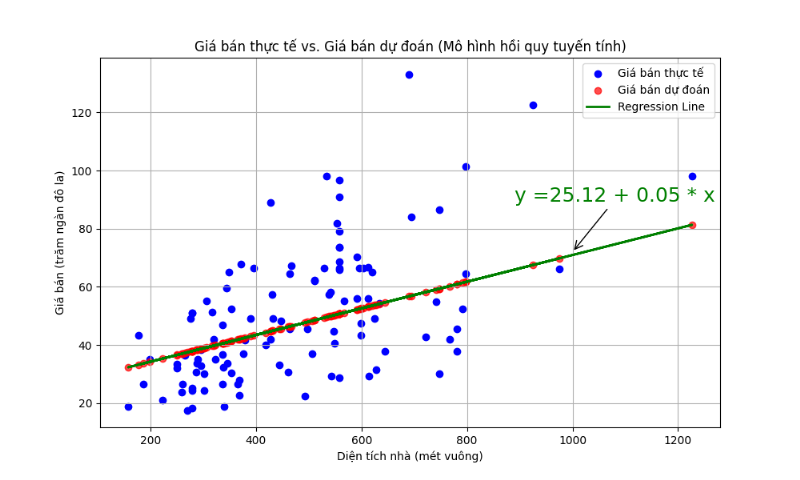
Hồi quy là một kỹ thuật thống kê cho phép chúng ta mô tả mối quan hệ giữa biến số phụ thuộc (Y) và một hoặc nhiều biến số độc lập (X). Nói cách khác, hồi quy giúp chúng ta dự đoán giá trị của Y dựa trên giá trị của X. Ví dụ, dựa trên số giờ học, chúng ta có thể dự đoán điểm thi của học sinh. Hay dựa trên diện tích nhà, chúng ta có thể dự đoán giá trị của căn nhà đó.
Mô hình hồi quy tuyến tính đơn giản
Mô hình hồi quy tuyến tính đơn giản là trường hợp đơn giản nhất, chỉ có một biến độc lập. Công thức của nó là: Y = a + bX, trong đó:
- Y là biến số phụ thuộc.
- X là biến số độc lập.
- a là hệ số chặn (intercept).
- b là hệ số góc (slope).
Bài tập tương quan và hồi quy có đáp án: Thực hành để nắm vững kiến thức
Bây giờ, chúng ta sẽ cùng nhau giải quyết một số bài tập tương quan và hồi quy có đáp án để củng cố kiến thức đã học.
Bài tập 1: Tính hệ số tương quan
Cho dữ liệu về chiều cao (cm) và cân nặng (kg) của 5 người:
| Chiều cao (cm) | Cân nặng (kg) |
|---|---|
| 160 | 55 |
| 170 | 65 |
| 180 | 75 |
| 165 | 60 |
| 175 | 70 |
Hãy tính hệ số tương quan Pearson giữa chiều cao và cân nặng. Đáp án: (Bạn cần sử dụng công thức tính hệ số tương quan Pearson để tính toán kết quả)
Bài tập 2: Xây dựng mô hình hồi quy
Cho dữ liệu về số giờ học (X) và điểm thi (Y) của 10 học sinh:
| Số giờ học (X) | Điểm thi (Y) |
|---|---|
| 2 | 5 |
| 4 | 7 |
| 6 | 9 |
| 8 | 11 |
| 10 | 13 |
| 3 | 6 |
| 5 | 8 |
| 7 | 10 |
| 9 | 12 |
| 11 | 14 |
Hãy xây dựng mô hình hồi quy tuyến tính đơn giản để dự đoán điểm thi dựa trên số giờ học. Đáp án: (Bạn cần sử dụng phương pháp hồi quy tuyến tính đơn giản để tìm ra các hệ số a và b trong công thức Y = a + bX)
 Bài tập hồi quy tuyến tính với đáp án
Bài tập hồi quy tuyến tính với đáp án
Những câu hỏi thường gặp về bài tập tương quan và hồi quy
Làm thế nào để chọn mô hình hồi quy phù hợp?
Việc chọn mô hình hồi quy phụ thuộc vào nhiều yếu tố, bao gồm: tính chất của dữ liệu, mối quan hệ giữa các biến, mục tiêu của nghiên cứu. Có nhiều loại mô hình hồi quy khác nhau, như hồi quy tuyến tính đa biến, hồi quy phi tuyến tính, hồi quy logistic…
Tôi có thể sử dụng phần mềm nào để tính toán tương quan và hồi quy?
Bạn có thể sử dụng nhiều phần mềm thống kê khác nhau như SPSS, R, Python (với thư viện Scikit-learn)… để tính toán tương quan và hồi quy một cách nhanh chóng và chính xác.
Những sai lầm thường gặp khi thực hiện bài tập tương quan và hồi quy là gì?
Một số sai lầm thường gặp bao gồm: không kiểm tra tính giả định của mô hình, không xử lý dữ liệu ngoại lai, không hiểu rõ ý nghĩa của các hệ số trong mô hình.
 Phần mềm hỗ trợ tính toán hồi quy
Phần mềm hỗ trợ tính toán hồi quy
Kết luận: Thực hành để thành thạo
Qua bài viết này, chúng ta đã cùng nhau tìm hiểu về tương quan và hồi quy, và thực hành giải quyết một số bài tập tương quan và hồi quy có đáp án. Hãy nhớ rằng, việc thực hành thường xuyên là chìa khóa để thành thạo các kỹ năng thống kê này. Hãy tiếp tục luyện tập với nhiều bài tập khác nhau, và đừng ngần ngại tìm kiếm thêm thông tin từ các nguồn uy tín để nâng cao kiến thức của mình. Chúc bạn thành công!