Nội dung bài viết
Phương Trình Lượng Giác Nâng Cao là một chủ đề quan trọng và thú vị trong toán học, đòi hỏi sự tư duy logic và kỹ năng biến đổi linh hoạt. Nếu bạn đang tìm kiếm cách chinh phục những bài toán lượng giác “khó nhằn”, thì bài viết này chính là dành cho bạn. Chúng ta sẽ cùng nhau khám phá những phương pháp giải quyết, ví dụ minh họa, và những “bí kíp” giúp bạn tự tin hơn khi đối mặt với phương trình lượng giác nâng cao.
Mục Lục
Phương Trình Lượng Giác Nâng Cao: Từ Cơ Bản Đến Nâng Cao
Để giải quyết phương trình lượng giác nâng cao, việc nắm vững kiến thức cơ bản là điều kiện tiên quyết. Hãy cùng ôn lại một số khái niệm quan trọng trước khi bước vào phần “nặng đô” hơn nhé!
Ôn Tập Kiến Thức Cơ Bản Về Lượng Giác
Câu hỏi thường gặp: Ôn tập kiến thức cơ bản về lượng giác như thế nào?
Tóm tắt: Việc ôn tập bao gồm nắm vững các công thức lượng giác cơ bản, bảng giá trị lượng giác của các góc đặc biệt (0, 30, 45, 60, 90 độ), và các mối quan hệ giữa các hàm lượng giác.
Các công thức lượng giác cơ bản như sin(a+b), cos(a+b), tan(a+b),… là nền tảng để giải quyết các bài toán phức tạp hơn. Bảng giá trị lượng giác của các góc đặc biệt giúp bạn tính toán nhanh chóng và chính xác. Việc hiểu rõ mối quan hệ giữa các hàm lượng giác như sin²x + cos²x = 1 cũng rất quan trọng.
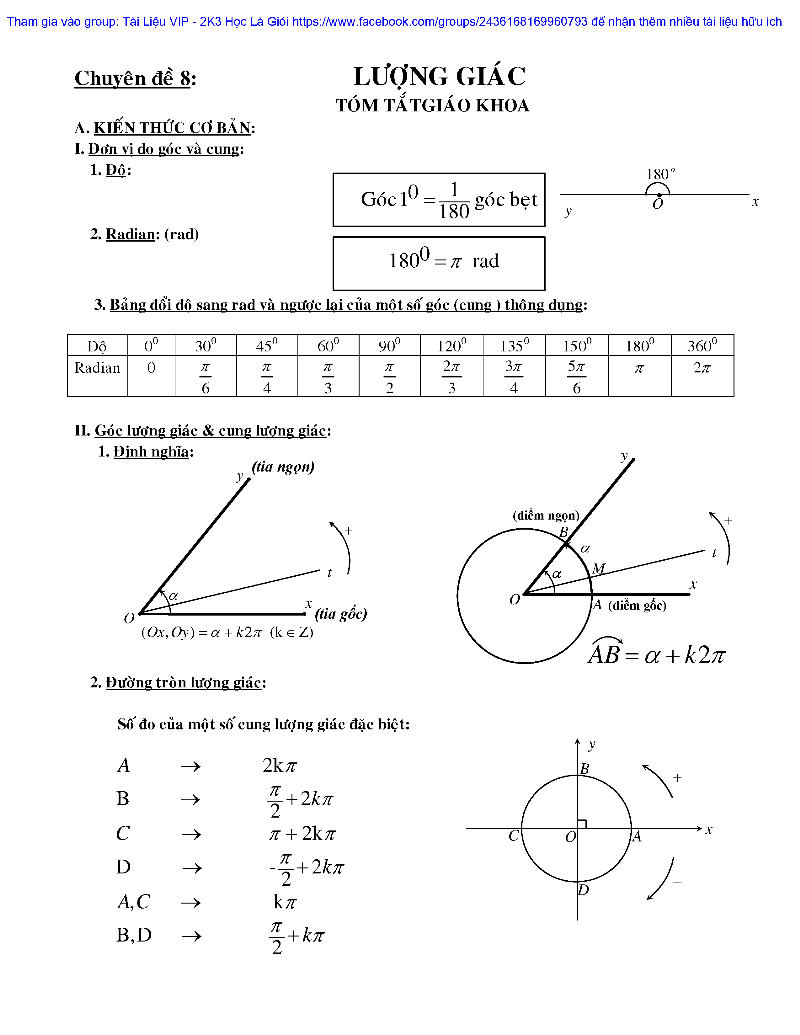Ôn tập kiến thức cơ bản về lượng giác
Các Dạng Phương Trình Lượng Giác Thường Gặp
Câu hỏi thường gặp: Các dạng phương trình lượng giác thường gặp là gì?
Tóm tắt: Các dạng phương trình lượng giác thường gặp bao gồm phương trình bậc nhất, bậc hai đối với một hàm lượng giác, phương trình dạng asinx + bcosx = c, và phương trình đối xứng, phản đối xứng.
Mỗi dạng phương trình đều có phương pháp giải quyết riêng. Ví dụ, phương trình bậc nhất sinx = a có thể giải bằng cách sử dụng hàm arcsin. Phương trình bậc hai cos²x + cosx – 2 = 0 có thể giải bằng cách đặt t = cosx.
Các dạng phương trình lượng giác thường gặp
Tương tự như [kỹ năng lập kế hoạch], việc phân loại các dạng phương trình lượng giác giúp chúng ta có cách tiếp cận bài toán một cách hiệu quả hơn.
Phương Pháp Giải Phương Trình Lượng Giác Nâng Cao
Sử Dụng Công Thức Biến Đổi Tổng Thành Tích, Tích Thành Tổng
Câu hỏi thường gặp: Khi nào nên sử dụng công thức biến đổi tổng thành tích, tích thành tổng?
Tóm tắt: Sử dụng công thức biến đổi tổng thành tích, tích thành tổng khi phương trình chứa tổng hoặc tích của các hàm lượng giác.
Công thức biến đổi tổng thành tích và tích thành tổng là “vũ khí bí mật” giúp bạn “đơn giản hóa” các phương trình phức tạp. Hãy tưởng tượng việc biến đổi sinx + cosx thành một dạng gọn gàng hơn, giúp bạn dễ dàng tìm ra nghiệm.
Đặt Ẩn Phụ
Câu hỏi thường gặp: Khi nào nên đặt ẩn phụ trong phương trình lượng giác?
Tóm tắt: Đặt ẩn phụ khi phương trình có dạng bậc cao hoặc chứa nhiều hàm lượng giác khác nhau.
Đặt ẩn phụ là một kỹ thuật hữu ích để “giảm nhẹ” độ phức tạp của phương trình. Ví dụ, nếu bạn gặp phương trình sin²x + 2sinxcosx + cos²x = 1, bạn có thể đặt t = sinx + cosx để đưa về phương trình bậc hai theo t.
Đặt ẩn phụ trong phương trình lượng giác
Giống như [việc làm thêm ca tối], việc đặt ẩn phụ đòi hỏi sự khéo léo và kinh nghiệm để chọn ẩn phụ phù hợp.
Hạ Bậc
Câu hỏi thường gặp: Làm thế nào để hạ bậc trong phương trình lượng giác?
Tóm tắt: Sử dụng công thức hạ bậc để giảm bậc của hàm lượng giác, ví dụ như biến đổi sin²x thành (1-cos2x)/2.
Hạ bậc là một phương pháp quan trọng giúp bạn “thuần hóa” những phương trình chứa hàm lượng giác bậc cao. Bằng cách hạ bậc, bạn có thể đưa phương trình về dạng dễ giải hơn.
Hạ bậc trong phương trình lượng giác
Việc hạ bậc cũng giống như việc tìm hiểu [khối c thi những môn nào], cần sự tỉ mỉ và chính xác.
Ví Dụ Minh Họa
Giải phương trình: sin2x + cos2x = √2sin(x + π/4)
Ta có: sin2x + cos2x = √2(sinxcos(π/4) + cosxsin(π/4)) = √2(sinx(√2/2) + cosx(√2/2)) = sinx + cosx
Vậy phương trình trở thành: sinx + cosx = √2sin(x + π/4)
Đặt t = x + π/4, ta có: sin(t – π/4) + cos(t – π/4) = √2sint
⇔ √2sin(t – π/4 + π/4) = √2sint
⇔ √2sint = √2sint (luôn đúng)
Vậy phương trình có nghiệm x ∈ R.
Bài Tập Thực Hành
Giải các phương trình sau:
- 2sin²x + 3sinxcosx + cos²x = 2
- sin3x + cos3x = cosx – sinx
Kết Luận
Phương trình lượng giác nâng cao không còn là “nỗi ám ảnh” nếu bạn nắm vững các phương pháp giải quyết và luyện tập thường xuyên. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức bổ ích và những “bí kíp” hữu ích để chinh phục những bài toán “khó nhằn”. Hãy thử áp dụng những kiến thức đã học và chia sẻ trải nghiệm của bạn với chúng tôi nhé!
Bài tập thực hành phương trình lượng giác nâng cao
Việc giải bài tập thực hành cũng tương tự như việc tính toán [chi phí xây nhà 2 tầng 80m2 ở nông thôn], đòi hỏi sự cẩn thận và chính xác.
Kết luận về phương trình lượng giác nâng cao
Việc học phương trình lượng giác cũng như việc xem [tử vi tuổi giáp thìn nữ mạng năm 2023], cần sự kiên trì và tìm tòi.
