Tổng hợp công thức xác suất thống kê: Hướng dẫn chi tiết cho người mới bắt đầu

Bạn đang tìm kiếm một nguồn tài liệu tổng hợp đầy đủ các công thức xác suất thống kê? Đừng lo lắng, bài viết này sẽ cung cấp cho bạn một “kho tàng” kiến thức về Tổng Hợp Công Thức Xác Suất Thống Kê, từ những khái niệm cơ bản nhất cho đến những công thức phức tạp hơn, tất cả được trình bày một cách dễ hiểu và minh bạch. Chúng ta sẽ cùng nhau khám phá thế giới thú vị của xác suất thống kê, từ những ví dụ đời thường đến các ứng dụng thực tiễn.

Khái niệm cơ bản về xác suất và thống kê

Trước khi đi sâu vào các công thức, hãy cùng làm rõ khái niệm cơ bản về xác suất và thống kê. Xác suất là thước đo khả năng xảy ra của một sự kiện. Ví dụ, xác suất tung đồng xu được mặt ngửa là 1/2, hoặc 50%. Thống kê, mặt khác, là việc thu thập, phân tích, diễn giải và trình bày dữ liệu. Nó giúp chúng ta hiểu rõ hơn về hiện tượng đang nghiên cứu. Cả xác suất và thống kê đều là những công cụ mạnh mẽ để hiểu và dự đoán thế giới xung quanh chúng ta.

Các công thức xác suất cơ bản

Xác suất của một sự kiện

Công thức xác suất của một sự kiện A được tính như sau:

P(A) = Số kết quả thuận lợi cho A / Tổng số kết quả có thể xảy ra

Ví dụ: Xác suất rút được quân Át từ bộ bài 52 lá là 4/52 = 1/13.

Xác suất của sự kiện đối lập

Xác suất của sự kiện đối lập của A (ký hiệu là A’) được tính:

P(A’) = 1 – P(A)

Ví dụ: Nếu xác suất trời mưa là 0.3, thì xác suất trời không mưa là 1 – 0.3 = 0.7.

Xác suất của hai sự kiện độc lập

Nếu hai sự kiện A và B là độc lập, xác suất cả hai sự kiện cùng xảy ra là:

P(A và B) = P(A) * P(B)

Ví dụ: Tung một đồng xu hai lần, xác suất được hai mặt ngửa là (1/2) * (1/2) = 1/4.

Xác suất có điều kiện

Xác suất của sự kiện A xảy ra, biết rằng sự kiện B đã xảy ra, được gọi là xác suất có điều kiện và được tính:

P(A|B) = P(A và B) / P(B)

Ví dụ: Trong một lớp học có 20 học sinh, 10 học sinh nam và 10 học sinh nữ. Trong số 10 học sinh nam, có 5 học sinh thích bóng đá. Xác suất một học sinh thích bóng đá, biết rằng học sinh đó là nam là 5/10 = 1/2.

Phân phối xác suất

Phân phối nhị thức

Phân phối nhị thức mô tả xác suất của số lần thành công trong một số lượng cố định của thử nghiệm Bernoulli độc lập. Công thức xác suất khối của phân phối nhị thức là:

P(X=k) = (nCk) p^k (1-p)^(n-k)

trong đó:

• n là số lượng thử nghiệm
• k là số lần thành công
• p là xác suất thành công trong mỗi thử nghiệm
• nCk là tổ hợp chập k của n, tính bằng n! / (k! * (n-k)!)

Phân phối Poisson

Phân phối Poisson mô tả xác suất của số lần xuất hiện của một sự kiện trong một khoảng thời gian hoặc không gian nhất định, nếu các sự kiện xảy ra độc lập với nhau và với tốc độ trung bình không đổi. Công thức xác suất khối của phân phối Poisson là:

P(X=k) = (λ^k * e^(-λ)) / k!

trong đó:

• k là số lần xuất hiện của sự kiện
• λ là tốc độ trung bình của sự kiện

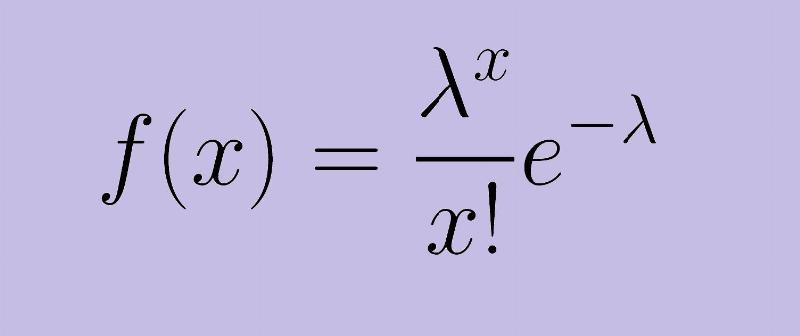bieu-do-phan-phoi-poisson

Phân phối chuẩn

Phân phối chuẩn là một trong những phân phối xác suất quan trọng nhất trong thống kê. Nó được đặc trưng bởi hai tham số: trung bình (μ) và độ lệch chuẩn (σ). Hàm mật độ xác suất của phân phối chuẩn là:

f(x) = (1 / (σ √(2π))) e^(-(x-μ)^2 / (2σ^2))

Thống kê mô tả

Thống kê mô tả bao gồm việc tóm tắt và trình bày dữ liệu. Một số chỉ số thống kê mô tả quan trọng bao gồm:

• Trung bình (Mean): Tổng các giá trị chia cho số lượng giá trị.
• Trung vị (Median): Giá trị ở giữa khi dữ liệu được sắp xếp theo thứ tự.
• Mốt (Mode): Giá trị xuất hiện nhiều nhất.
• Độ lệch chuẩn (Standard Deviation): Đo lường sự phân tán của dữ liệu xung quanh trung bình.
• Phương sai (Variance): Bình phương của độ lệch chuẩn.

Kiểm định giả thuyết

Kiểm định giả thuyết là một quá trình thống kê để kiểm tra xem có đủ bằng chứng để bác bỏ một giả thuyết nào đó hay không. Một số kiểm định giả thuyết thường gặp bao gồm:

• Kiểm định t: Được sử dụng để so sánh trung bình của hai nhóm độc lập hoặc kiểm tra xem trung bình mẫu có khác biệt đáng kể so với một giá trị nào đó hay không.
• Kiểm định Z: Tương tự như kiểm định t, nhưng được sử dụng khi kích thước mẫu lớn.
• Kiểm định χ² (Chi-square): Được sử dụng để kiểm tra sự độc lập giữa hai biến định tính hoặc để kiểm tra xem phân phối quan sát có phù hợp với phân phối lý thuyết hay không.
• Kiểm định ANOVA (Analysis of Variance): Được sử dụng để so sánh trung bình của ba nhóm hoặc nhiều nhóm hơn.

Ứng dụng của xác suất thống kê

Xác suất thống kê được ứng dụng rộng rãi trong nhiều lĩnh vực, bao gồm:

• Nghiên cứu khoa học: Để phân tích dữ liệu, kiểm định giả thuyết và rút ra kết luận.
• Kinh tế: Để dự báo xu hướng thị trường, đánh giá rủi ro và đưa ra quyết định đầu tư.
• Y tế: Để thiết kế các thử nghiệm lâm sàng, phân tích kết quả và đánh giá hiệu quả của phương pháp điều trị.
• Kỹ thuật: Để kiểm soát chất lượng, tối ưu hóa quy trình sản xuất và dự đoán tuổi thọ của sản phẩm.
• Quản lý rủi ro: Xác định, đánh giá và giảm thiểu rủi ro trong các hoạt động kinh doanh.

Làm thế nào để áp dụng công thức xác suất thống kê vào báo cáo thực tập?

Việc áp dụng công thức xác suất thống kê vào báo cáo thực tập của bạn phụ thuộc rất nhiều vào lĩnh vực bạn đang nghiên cứu. Tuy nhiên, một số ví dụ điển hình bao gồm:

• Phân tích dữ liệu khảo sát: Sử dụng phân phối nhị thức hoặc phân phối chuẩn để phân tích dữ liệu từ các bảng câu hỏi. Ví dụ, bạn có thể dùng để xác định tỷ lệ khách hàng hài lòng với một sản phẩm hoặc dịch vụ.
• Phân tích dữ liệu kinh doanh: Sử dụng các chỉ số thống kê mô tả (trung bình, độ lệch chuẩn,…) để tóm tắt dữ liệu doanh số, lợi nhuận, chi phí, v.v. Bạn cũng có thể dùng phân phối Poisson để mô hình hóa số lượng khách hàng đến cửa hàng trong một khoảng thời gian nhất định.
• Nghiên cứu thị trường: Áp dụng các kiểm định giả thuyết để kiểm tra xem có sự khác biệt đáng kể giữa hai nhóm khách hàng hay không (ví dụ, nhóm sử dụng sản phẩm A và nhóm sử dụng sản phẩm B).
• Dự đoán xu hướng: Sử dụng các mô hình hồi quy để dự đoán doanh số bán hàng trong tương lai dựa trên dữ liệu lịch sử.

Nhớ rằng, để sử dụng hiệu quả các công thức này, bạn cần hiểu rõ ý nghĩa của từng công thức và cách áp dụng chúng vào từng tình huống cụ thể. Hãy tham khảo thêm các tài liệu chuyên ngành và tìm kiếm sự hỗ trợ từ giáo viên hoặc người hướng dẫn nếu cần thiết.

Câu hỏi thường gặp về tổng hợp công thức xác suất thống kê

Tôi nên bắt đầu học xác suất thống kê từ đâu?

Bạn nên bắt đầu bằng cách nắm vững các khái niệm cơ bản về xác suất và thống kê, sau đó dần dần tìm hiểu các công thức và kỹ thuật phân tích dữ liệu. Có rất nhiều tài liệu học tập trực tuyến và sách giáo khoa có thể giúp bạn. Hãy bắt đầu với những ví dụ đơn giản và dần dần chuyển sang các bài toán phức tạp hơn.

Có công cụ nào hỗ trợ tính toán xác suất thống kê không?

Có rất nhiều phần mềm thống kê có thể giúp bạn tính toán xác suất và thực hiện các phân tích thống kê, ví dụ như SPSS, R, Python (với thư viện SciPy, Statsmodels). Bạn cũng có thể sử dụng các máy tính cầm tay hoặc các trang web trực tuyến để tính toán các công thức cơ bản.

Làm thế nào để chọn công thức xác suất thống kê phù hợp?

Việc lựa chọn công thức xác suất thống kê phù hợp phụ thuộc vào loại dữ liệu bạn đang làm việc, mục tiêu phân tích của bạn và các giả định về dữ liệu. Hãy tham khảo các tài liệu chuyên ngành hoặc tìm kiếm sự hỗ trợ từ người có kinh nghiệm để lựa chọn công thức phù hợp.

Kết luận

Tổng hợp công thức xác suất thống kê này hy vọng sẽ giúp bạn có cái nhìn tổng quan về các công cụ và kỹ thuật quan trọng trong lĩnh vực này. Việc nắm vững các công thức và kỹ thuật này sẽ giúp bạn giải quyết được nhiều bài toán thực tiễn và tạo ra những báo cáo thực tập chất lượng cao. Hãy bắt đầu thực hành và áp dụng những kiến thức đã học vào các bài tập thực tế để củng cố kiến thức của bạn. Chúc bạn thành công! Bạn có thể tìm hiểu thêm về báo cáo thực tập kế toán hàng tồn kho để áp dụng những kiến thức này vào thực tế. Hoặc tham khảo thêm về biểu đồ tuần tự quản lý bán hàng để có cái nhìn tổng quan hơn về việc áp dụng thống kê trong kinh doanh. Nếu bạn đang tìm việc, hãy tham khảo tìm việc làm nhân viên nhập liệu hoặc tuyển nhân viên kho tphcm. Bạn cũng có thể tham khảo bản vẽ cánh tay robot để hiểu rõ hơn về ứng dụng của thống kê trong kỹ thuật.